Question

已知点A在数轴上对应的数是a，点B在数轴上对应的数是b，且|a+4|+（b-1）²=0．现将A、B之间的距离记作|AB|，定义|AB|=|a-b|．
（1）|AB|=

5

；
（2）设点P在数轴上对应的数是x，当|PA|-|PB|=2时，求x的值．

Answer 1

分析：（1）根据非负数的和为0，各项都为0；
（2）应考虑到A、B、P三点之间的位置关系的多种可能解题．

解答：解：（1）∵|a+4|+（b-1）²=0，
∴a=-4，b=1，
∴|AB|=|a-b|=5；

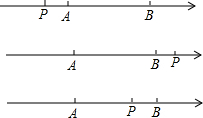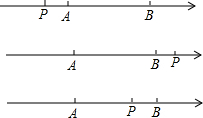（2）当P在点A左侧时，
|PA|-|PB|=-（|PB|-|PA|）=-|AB|=-5≠2．
当P在点B右侧时，
|PA|-|PB|=|AB|=5≠2．
∴上述两种情况的点P不存在．
当P在A、B之间时，|PA|=|x-（-4）|=x+4，|PB|=|x-1|=1-x，
∵|PA|-|PB|=2，∴x+4-（1-x）=2．
∴x=-

1

2

，即x的值为-

1

2

；
故答案为：5．

点评：本题渗透了分类讨论的思想，体现了思维的严密性，在今后解决类似的问题时，要防止漏解．同时，灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点．