题目内容
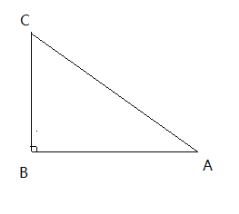
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm。
(1)若P、Q是△ABC边上的两个动点,其中点P从A沿A→B方向运动,速度为每秒1cm,点Q从B沿B→C方向运动,速度为每秒2cm,两点同时出发,设出发时间为t秒.①当t=1秒时,求PQ的长;②从出发几秒钟后,△PQB是等腰三角形?
(2)若M在△ABC边上沿B→A→C方向以每秒3cm的速度运动,则当点M在边CA上运动时,求△BCM成为等腰三角形时M运动的时间.
【答案】(1)、PQ=![]() ;(2)、t=
;(2)、t=![]() ;t=2、t=
;t=2、t=![]() 、t=4
、t=4
【解析】
试题分析:(1)、根据t的值得出AP,BP和BQ的长度,然后根据勾股定理得出答案;(2)、对于动点,首先将动点所产生的线段用含t的代数式来表示,然后根据勾股定理以及等腰三角形的性质求出t的值.
试题解析:(1)、∵当t=1时,AP=1,BP=7,BQ=2 ∴PQ=![]()
(2)、∵△PQB是等腰三角形,∠B=90° ∴BP=BQ BP=8-t, BQ=2t
∴8-t=2t 解得t=![]()
(3)、当BC=BM时,t=2 当MC=MB时,t=![]() 当CB=CM时,t=4
当CB=CM时,t=4

练习册系列答案
相关题目