题目内容
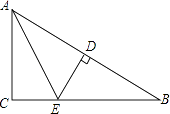
【题目】如图,在四边形ABCD中,AC平分∠DAE,DA∥CE,AB=CB. 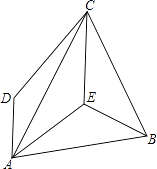
(1)试判断BE与AC有何位置关系?并证明你的结论;
(2)若∠DAC=25°,求∠AEB的度数.
【答案】
(1)位置关系:BE垂直平分AC,
证明:∵AC平分∠DAE,
∴∠DAC=∠EAC,
∵DA∥CE,
∴∠DAC=∠ACE,
∴∠ACE=∠EAC,
∴EA=EC,
∴E在AC的垂直平分线上,
∵AB=CB,
∴B在AC的垂直平分线上,
∴BE垂直平分AC
(2)解:∵AC是∠DAE的平分线,
∴∠DAC=∠CAE=25°,
又∵DA∥E
∴∠DAC=∠ACE=25°
∴∠CAE=∠ACE=25°
∴AE=CE,∠AEC=130°,
在△AEB和△CEB中,
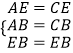 ,
,
∴△AEB≌△CEB,
∴∠AEB=∠CEB,
∴∠AEB= ![]() (360°﹣∠AEC)=115°
(360°﹣∠AEC)=115°
【解析】(1)由∠DAC=∠EAC,DA∥CE,可得∠DAC=∠ACE,可推出∠ACE=∠EAC,得到EA=EC,可证得BE在AC的垂直平分线上,由AB=CB,可证得结论;(2)由已知AC是∠DAE的平分线可推出∠EAC=∠DAC,由DA∥CE可推出∠ECA=∠DAC,所以得到∠EAC=∠ECA,则AE=CE,又已知∠AEB=∠CEB,BE=BE,因此△AEB≌△CEB,问题得解.

练习册系列答案
相关题目