题目内容
【题目】2016年里约奥运会,中国跳水队赢得8个项目中的7块金牌,优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系. 
(1)当k=4时,求这条抛物线的解析式;
(2)当k=4时,求运动员落水点与点C的距离;
(3)图中CE= ![]() 米,CF=
米,CF= ![]() 米,若跳水运动员在区域EF内(含点E,F)入水时才能达到训练要求,求k的取值范围.
米,若跳水运动员在区域EF内(含点E,F)入水时才能达到训练要求,求k的取值范围.
【答案】
(1)解:如图所示:
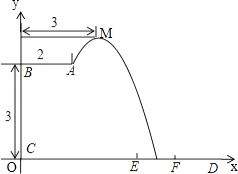
根据题意,可得抛物线顶点坐标M(3,4),A(2,3)
设抛物线解析为:y=a(x﹣3)2+4,
则3=a(2﹣3)2+4,
解得:a=﹣1,
故抛物线解析式为:y=﹣(x﹣3)2+4
(2)解:由题意可得:当y=0,则0=﹣(x﹣3)2+4,
解得:x1=1,x2=5,
故抛物线与x轴交点为:(5,0),
当k=4时,求运动员落水点与点C的距离为5米
(3)解:根据题意,抛物线解析式为:y=a(x﹣3)2+k,
将点A(2,3)代入可得:a+k=3,即a=3﹣k
若跳水运动员在区域EF内(含点E,F)入水,
则当x= ![]() 时,y=
时,y= ![]() a+k≥0,即
a+k≥0,即 ![]() (3﹣k)+k≥0,
(3﹣k)+k≥0,
解得:k≤ ![]() ,
,
当x= ![]() 时,y=
时,y= ![]() a+k≤0,即
a+k≤0,即 ![]() (3﹣k)+k≤0,
(3﹣k)+k≤0,
解得:k≥ ![]() ,
,
故 ![]() ≤k≤
≤k≤ ![]()
【解析】(1)根据抛物线顶点坐标M(3,4),可设抛物线解析为:y=a(x﹣3)2+4,将点A(2,3)代入可得;(2)在(1)中函数解析式中令y=0,求出x即可;(3)若跳水运动员在区域EF内(含点E,F)入水达到训练要求,则在函数y=a(x﹣3)2+k中当x= ![]() 米,y>0,当x=
米,y>0,当x= ![]() 米时y<0,解不等式即可得.
米时y<0,解不等式即可得.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案