题目内容
【题目】如图,抛物线y=x2+bx+c与x轴分别交于A(1,0),B(5,0)两点.
(1)求抛物线的解析式;
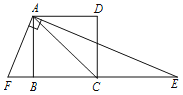
(2)过点C(﹣3,0)在x轴下方作x轴的垂线,再以点A为圆心、5为半径长画弧,交先前所作垂线于D,连接AD(如图),将Rt△ACD沿x轴向右平移m个单位,当点D落在抛物线上时,求m的值;
(3)在(2)的条件下,当点D第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.

【答案】(1)y=x2﹣6x+5;(2)m的值为5或7;(3)Q点的坐标为(4,﹣3)或(0,5)或(6,5).
【解析】分析:(1)直接利用交点式可写出抛物线的解析式;
(2)利用勾股定理计算出CD,则可确定D(-3,-3),过点D作x轴的平行线交抛物线于点E、F,如图,解方程x2-6x+5=-3得到E(2,-3),F(4,-3),然后确定Rt△ACD沿x轴向左平移的距离,从而得到m的值;
(3)抛物线的对称轴为直线x=3,则P点的横坐标为3,E(2,-3),B(5,0),讨论:若四边形EBQP为平行四边形,利用平行四边形的性质和点平移的规律得到点Q的横坐标为6,则计算x=6对应的函数值得到此时Q点坐标;若四边形EBP′Q′为平行四边形或四边形EP″BQ″为平行四边形时,利用同样的方法可求出对应的Q点坐标.
详解:(1)抛物线的解析式为y=(x﹣1)(x﹣5),
即y=x2﹣6x+5;
(2)∵AD=5,AC=1+3=4,
∴CD=![]() =3,
=3,
∴D(﹣3,﹣3),
过点D作x轴的平行线交抛物线于点E、F,如图,
当y=﹣3时,x2﹣6x+5=﹣3,解得x1=2,x2=4,则E(2,﹣3),F(4,﹣3),
∴ED=2﹣(﹣3)=5,FD=4﹣(3)=7,
∴m的值为5或7;
(3)抛物线的对称轴为直线x=3,则P点的横坐标为3,E(2,﹣3),B(5,0),
若四边形EBQP为平行四边形,点E向右平移3个单位,向上平移3个单位得到B点,则点P向右平移3个单位,向上平移3个单位得到Q点,所以点Q的横坐标为6,当x=6时,y=x2﹣6x+5=5,此时Q(6,5);
若四边形EBP′Q′为平行四边形,点B向左平移3个单位,向下平移3个单位得到E点,则点P′向左平移3个单位,向下平移3个单位得到Q′点,所以点Q的横坐标为0,当x=0时,y=x2﹣6x+5=5,此时Q′(0,5);
若四边形EP″BQ″为平行四边形,点P″向左平移1个单位可得到E点,则点B向左平移1个单位可得到Q″点,所以点Q的横坐标为4,当x=4时,y=x2﹣6x+5=﹣3,此时Q′(4,﹣3),
综上所述,Q点的坐标为(4,﹣3)或(0,5)或(6,5).