题目内容
【题目】已知关于x的方程x2﹣kx+k2+n=0有两个不相等的实数根x1、x2,且(2x1+x2)2﹣8(2x1+x2)+15=0.
(1)求证:n<0;
(2)试用k的代数式表示x1;
(3)当n=﹣3时,求k的值.
【答案】(1)证明见解析;(2)x1=3﹣k或x1=5﹣k.(3)k=1.
【解析】
(1)方程有两个不相等的实数根,则△>0,建立关于n,k的不等式,由此即可证得结论;(2)根据根与系数的关系,把x1+x2=k代入已知条件(2x1+x2)2﹣8(2x1+x2)+15=0,即可用k的代数式表示x1;(3)首先由(1)知n<﹣![]() k2,又n=﹣3,求出k的范围.再把(2)中求得的关系式代入原方程,即可求出k的值.
k2,又n=﹣3,求出k的范围.再把(2)中求得的关系式代入原方程,即可求出k的值.
证明:(1)∵关于x的方程x2﹣kx+k2+n=0有两个不相等的实数根,
∴△=k2﹣4(k2+n)=﹣3k2﹣4n>0,
∴n<﹣![]() k2.
k2.
又﹣k2≤0,
∴n<0.
解:(2)∵(2x1+x2)2﹣8(2x1+x2)+15=0,x1+x2=k,
∴(x1+x1+x2)2﹣8(x1+x1+x2)+15=0
∴(x1+k)2﹣8(x1+k)+15=0
∴[(x1+k)﹣3][(x1+k)﹣5]=0
∴x1+k=3或x1+k=5,
∴x1=3﹣k或x1=5﹣k.
(3)∵n<﹣![]() k2,n=﹣3,
k2,n=﹣3,
∴k2<4,即:﹣2<k<2.
原方程化为:x2﹣kx+k2﹣3=0,
把x1=3﹣k代入,得到k2﹣3k+2=0,
解得k1=1,k2=2(不合题意),
把x2=5﹣k代入,得到3k2﹣15k+22=0,△=﹣39<0,所以此时k不存在.
∴k=1.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案【题目】观察如图图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法,……,据此解答下面的问题
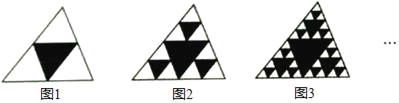
(1)填写下表:
图形 | 挖去三角形的个数 |
图形1 | 1 |
图形2 | 1+3 |
图形3 | 1+3+9 |
图形4 |
|
(2)根据这个规律,求图n中挖去三角形的个数wn;(用含n的代数式表示)
(3)若图n+1中挖去三角形的个数为wn+1,求wn+1﹣Wn