题目内容
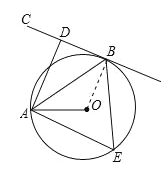
【题目】 如图,![]() 是
是![]() 的弦,
的弦,![]() 切
切![]() 于点
于点![]() 垂足为
垂足为![]() 是
是![]() 的半径,且
的半径,且![]() .
.
(1)求证:![]() 平分
平分![]() ;
;
(2)若点![]() 是优弧
是优弧![]() 上一点,且
上一点,且![]() ,求扇形
,求扇形![]() 的面积(计算结果保留
的面积(计算结果保留![]() )
)

【答案】(1)详见解析;(2)3π.
【解析】
试题分析:(1)连接OB,由切线的性质得出OB⊥BC,证出AD∥OB,由平行线的性质和等腰三角形的性质证出∠DAB=∠OAB,即可得出结论;(2)由圆周角定理得出∠AOB=120°,由扇形面积公式即可得出答案.
试题解析:
(1)证明:连接OB,如图所示:
∵BC切⊙O于点B,
∴OB⊥BC,
∵AD⊥BC,
∴AD∥OB,
∴∠DAB=∠OBA,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠DAB=∠OAB,
∴AB平分∠OAD;
(2)解:∵点E是优弧![]() 上一点,且∠AEB=60°,
上一点,且∠AEB=60°,
∴∠AOB=2∠AEB=120°,
∴扇形OAB的面积=![]() =3π.
=3π.

练习册系列答案
相关题目






