题目内容
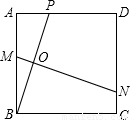
已知:如图,点P是边长为4的正方形ABCD的边AD上一点并且不与点A、D重合,MN是线段BP的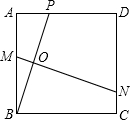 垂直平分线,与AB、BP、CD分别交于点M、O、N,设AP=x.
垂直平分线,与AB、BP、CD分别交于点M、O、N,设AP=x.(1)求BM(结果用含有x的代数式表示);
(2)请你判断四边形MNCB的面积是否有最小值?若有最小值,求出使其面积取得最小值时的x的值并求出面积的最小值;若没有最小值,说明你的理由.
分析:(1)首先由正方形的性质与线段垂直平分线的性质求得BP与OB的值,又由∠ABP是公共角,∠A=∠MOB,易得Rt△BOM∽Rt△BAP,根据相似三角形的对应边成比例,即可求得BM的长;
(2)首先作NE⊥AB于E,由(1)可得Rt△BOM∽Rt△BAP,则可证得:Rt△MNE≌Rt△PBA,即可求得CN的值,求得四边形MNCB的最大值.
(2)首先作NE⊥AB于E,由(1)可得Rt△BOM∽Rt△BAP,则可证得:Rt△MNE≌Rt△PBA,即可求得CN的值,求得四边形MNCB的最大值.
解答:解:(1)∵四边形ABCD是边长为4的正方形,MN是PB的垂直平分线,
∴∠A=90°,∠MOB=90°,OB=
BP,
∴BP=
=
,OB=
,
又∵∠ABP是公共角,∠A=∠MOB,
∴Rt△BOM∽Rt△BAP.
∴
=
,
即MB•AB=OB•PB,
∴4MB=
•
=
x2+8,
∴BM=
x2+2.
(2)四边形MNCB的面积有最小值.
作NE⊥AB于E,
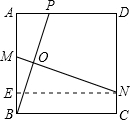 则∠MEN=∠BEN=90°=∠A,NE=BC=BA=4,
则∠MEN=∠BEN=90°=∠A,NE=BC=BA=4,
由(1)知Rt△BOM∽Rt△BAP,
∴∠NME=∠APB,
∴Rt△MNE≌Rt△PBA,
∴ME=PA=x,
∴CN=BE=MB-ME=
x2-x+2,
∴S四边形MNCB=
(CN+MB)•NE=
[(
x2-x+2)+(
x2+2)]•4=
(x-2)2+6,
∴当x=2时,四边形MNCB的面积有最小值6.
∴∠A=90°,∠MOB=90°,OB=
| 1 |
| 2 |
∴BP=
| 42+x2 |
| 16+x2 |
| 1 |
| 2 |
| 16+x2 |
又∵∠ABP是公共角,∠A=∠MOB,
∴Rt△BOM∽Rt△BAP.
∴
| OB |
| AB |
| MB |
| PB |
即MB•AB=OB•PB,
∴4MB=
| 1 |
| 2 |
| 16+x2 |
| 16+x2 |
| 1 |
| 2 |
∴BM=
| 1 |
| 8 |
(2)四边形MNCB的面积有最小值.
作NE⊥AB于E,
 则∠MEN=∠BEN=90°=∠A,NE=BC=BA=4,
则∠MEN=∠BEN=90°=∠A,NE=BC=BA=4,由(1)知Rt△BOM∽Rt△BAP,
∴∠NME=∠APB,
∴Rt△MNE≌Rt△PBA,
∴ME=PA=x,
∴CN=BE=MB-ME=
| 1 |
| 8 |
∴S四边形MNCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
∴当x=2时,四边形MNCB的面积有最小值6.
点评:本小题主要考查运用三角形相似解决相关的问题的能力与数形结合的能力以及运算能力.此题属综合性题目,属较难的题目,解题时要注意数形结合思想的应用.

练习册系列答案
相关题目
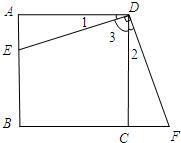 20、已知:如图,点E是正方形ABCD的边AB上任意一点,过点D作DF⊥DE交BC的延长线于点F.求证:DE=DF.
20、已知:如图,点E是正方形ABCD的边AB上任意一点,过点D作DF⊥DE交BC的延长线于点F.求证:DE=DF.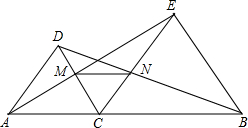 AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.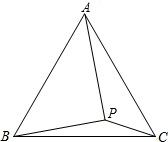 已知:如图,点P是等边三角形ABC内一点,
已知:如图,点P是等边三角形ABC内一点,