题目内容
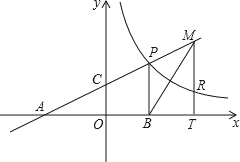
【题目】如图,直线AP的解析式y=kx+4k分别交于x轴、y轴于A、C两点,与反比例函数y=![]() (x>0)交于点P.且PB⊥x轴于B点,S△PAB=9.
(x>0)交于点P.且PB⊥x轴于B点,S△PAB=9.
(1)求一次函数解析式;
(2)点Q是x轴上的一动点,当QC+QP的值最小时,求Q点坐标;
(3)设点R与点P同在反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴于T点,交AC于点M,是否存在点R,使得△BTM与△AOC全等?若存在,求点R的坐标;若不存在,说明理由.
【答案】(1)直线AP解析式为y=![]() x+2;(2)Q(0.8,0);(3)R坐标为(4,1.5).
x+2;(2)Q(0.8,0);(3)R坐标为(4,1.5).
【解析】
(1)由直线AP解析式得到直线恒过A(-4,0),得到OA=4,设OB=a,PB=b,由P在反比例图象上得到ab=6,再由OA+OB表示出AB,根据AB与PB乘积的一半表示出三角形PAB面积,根据已知三角形PAB的面积求出a与b的值,确定出P坐标,将P代入直线AP解析式求出k的值即可;
(2)找出C关于x轴的对称点C′,连接PC′与x轴交于点Q,确定出直线PC′解析式,求出与x轴交点即可确定出Q坐标;
(3)由直线AP解析式求出OA与OC的长,若△BTM与△AOC全等,则有BT=OC,MT=OA,确定出M坐标,代入直线AP检验即可得到结果.
(1)直线AP解析式y=kx+4k=k(x+4),
得到A(﹣4,0),即OA=4,
设OB=a,PB=b,即P(a,b),
代入反比例解析式得:ab=6,
∵S△PAB=![]() ABPB=9,
ABPB=9,
∴![]() (a+4)b=9,即ab+4b=6+4b=18,
(a+4)b=9,即ab+4b=6+4b=18,
解得:a=2,b=3,即P(2,3),
将P(2,3)代入直线y=kx+4k中得:3=2k+4k,
解得:k=![]() ,
,
则直线AP解析式为y=![]() x+2;
x+2;
(2)对于直线y=![]() x+2,令x=0,得到y=2,即C(0,2),OC=2,
x+2,令x=0,得到y=2,即C(0,2),OC=2,
找出C关于x轴的对称点C′(0,﹣2),连接PC′,交x轴与Q点,此时QC+QP最短,
设直线C′P解析式为y=mx+n,
将P(2,3)与C′(0,﹣2)代入得:![]() ,
,
解得:m=2.5,n=﹣2,
∴直线C′P解析式为y=2.5x﹣2,
令y=0,得到x=0.8,即Q(0.8,0);
(3)若△BTM≌△COA,则有BT=OC=2,MT=OA=4,
∴OT=OB+BT=2+2=4,即M(4,4),
将x=4代入直线OP解析式得:y=![]() ×4+2=2+2=4,即M在直线AP上,
×4+2=2+2=4,即M在直线AP上,
将x=4代入反比例解析式得:y=![]() =1.5,
=1.5,
此时R坐标为(4,1.5).