题目内容
【题目】如图,正方形ABCD的边长为8,E为BC上一定点,BE=6,F为AB上一动点,把△BEF沿EF折叠,点B落在点B′处,当△AFB′恰好为直角三角形时,B′D的长为?

【答案】![]() 或
或![]()
【解析】
分两种情况如图1,当∠AB′F=90°时,此时A、B′、E三点共线,过点B′作B′M⊥AB,B′N⊥AD,由三角形的面积法则可求得B′M=2.4,再由勾股定理可求得B′N=3.2,在Rt△CB′N中,由勾股定理得,B′D=![]() ;如图2,当∠AFB′=90°时,由题意可知此时四边形EBFB′是正方形,AF=2,过点B′作B′N⊥AD,则四边形AFB′N为矩形,在Rt△CB′N中,由勾股定理得,B′D=
;如图2,当∠AFB′=90°时,由题意可知此时四边形EBFB′是正方形,AF=2,过点B′作B′N⊥AD,则四边形AFB′N为矩形,在Rt△CB′N中,由勾股定理得,B′D=![]() ;
;
如图1,当∠AB′F=90°时,此时A、B′、E三点共线,
∵∠B=90°,∴AE=![]() =10,
=10,
∵B′E=BE=6,∴AB′=4,
∵B′F=BF,AF+BF=AB=8,
在Rt△AB′F中,∠AB′F=90°,由勾股定理得,AF2=FB′2+AB′2,
∴AF=5,BF=3,
过点B′作B′M⊥AB,B′N⊥AD,由三角形的面积法则可求得B′M=2.4,再由勾股定理可求得B′N=3.2,
∴AN=B′M=2.4,∴DN=AD-AN=8-2.4=5.6,
在Rt△CB′N中,由勾股定理得,B′D=![]() =
=![]() ;
;

如图2,当∠AFB′=90°时,由题意可知此时四边形EBFB′是正方形,∴AF=2,
过点B′作B′N⊥AD,则四边形AFB′N为矩形,∴AN=B′F=6,B′N=AF=2,∴DN=AD-AN=2,
在Rt△CB′N中,由勾股定理得,B′D=![]() =
=![]() ;
;
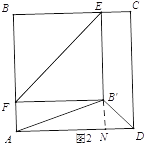
综上,可得B′D的长为![]() 或
或![]() .
.

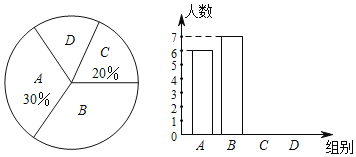
【题目】某中学抽取了40名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
组别 | 时间/小时 | 频数/人数 |
A组 |
| 2 |
B组 |
| m |
C组 |
| 10 |
D组 |
| 12 |
E组 |
| 7 |
F组 |
| 4 |
频数分布表
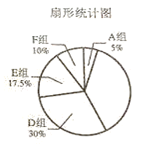
请根据图表中的信息解答下列问题:
(1)求频数分布表中m的值;
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角度数,并补全扇形统计图;
(3)已知F组的学生中,只有1名男生,其余都是女生,用列举法求以下事件的概率:从F组中随机选取2名学生,恰好都是女生。