��Ŀ����
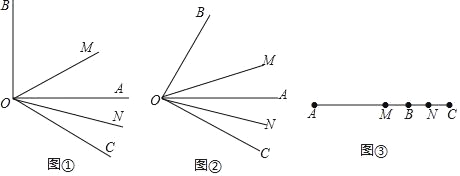
����Ŀ��������㣺��ͼ������AOB=90������AOCΪ��AOB���һ���ǣ��ҡ�AOC=30��������OMƽ�֡�BOC��ONƽ�֡�AOC�����MON�Ķ�����
��չ̽������ͼ������AOB=������AOC=������������Ϊ��ǣ�������OMƽ�֡�BOC��ONƽ�֡�AOC�����MON�Ķ�����
Ǩ��Ӧ�ã���ʵ�߶εļ�����ǵļ�������Ž��ܵ���ϵ����ͼ���߶�AB=m���ӳ��߶�AB��C��ʹ��BC=n����M��N�ֱ�ΪAC��BC���е㣬��MN�ij�Ϊ_____��ֱ��д���������
���𰸡�������㣺 ![]() ����չ̽����
����չ̽���� ![]() ��Ǩ��Ӧ�ã�
��Ǩ��Ӧ�ã� ![]() .
.
�����������������������㣺���ݽǵ�ƽ���ߵ��ص㣬���Ե�֪����������ȣ�����ԭ�ǵ�һ�룬���ݽ����֮���������ϵ���ɵó����ۣ�
��չ̽�������ݽǵ�ƽ���ߵ��ص㣬���Ե�֪����������ȣ�����ԭ�ǵ�һ�룬���ݽ����֮���������ϵ���ɵó����ۣ�
Ǩ��Ӧ�ã��������������ԭ����ͨ���Ƶ�����ֱ�ӣ��ó����ۣ�
���������������㣺�ߡ�BOC=��AOB+��AOC=90��+30��=120����
����OMƽ�֡�BOC��
���COM=![]() ��BOC=
��BOC=![]() ��120��=60����
��120��=60����
��ONƽ�֡�AOC��
���CON=![]() ��AOC=
��AOC=![]() ��30��=15����
��30��=15����
���MON=��COM����CON=60�㩁15��=45����
��չ̽�����ߡ�BOC=��AOB+��AOC=��+����
������OMƽ�֡�BOC��
���COM=![]() ��BOC=
��BOC=![]() ����+������
����+������
��ONƽ�֡�AOC��
���CON=![]() ��AOC=
��AOC=![]() ����
����
���MON=��COM����CON=![]() ����+������
����+������![]() ��=
��=![]() ����
����
Ǩ��Ӧ�ã���AB=m��BC=n��
��AC=AB+BC=m+n��
�ߵ�M��N�ֱ�ΪAC��BC���е㣬
��CM=![]() AC=
AC=![]() ��m+n����CN=
��m+n����CN=![]() BC=
BC=![]() n��
n��
��MN=CM��CN=![]() m��
m��
�ʴ�Ϊ�� ![]() m��
m��