题目内容
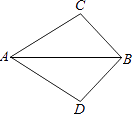
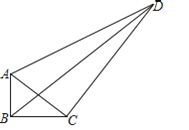
【题目】如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=![]() ,则下列结论:①AC⊥BD;②AC⊥CD;③tan∠DAC=2;④四边形ABCD的面积为31;⑤BD=2
,则下列结论:①AC⊥BD;②AC⊥CD;③tan∠DAC=2;④四边形ABCD的面积为31;⑤BD=2![]() .正确的是_______.
.正确的是_______.
【答案】②③④⑤
【解析】∵∠ABC=90°,AB=3,BC=4,
∴AC=![]() =5,
=5,
在△ACD中,∵CD=10,DA=![]() ,
,
∴AC+CD=25+100=125=DA,
∴∠ACD=90°,即AC⊥CD,故①错误,②正确;
在Rt△ACD中,tan∠DAC=![]() =
=![]() =2,故③正确;
=2,故③正确;
S四边形ABCD=![]() =
=![]() ABBC+
ABBC+![]() ACCD=
ACCD=![]() ×3×4+
×3×4+![]() ×5×10=31,
×5×10=31,
故④正确;
作DM⊥BC,交BC延长线于M,如图所示:
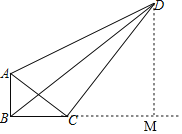
则∠M=90°,
∴∠DCM+∠CDM=90°,
∵∠ABC=90°,AB=3,BC=4,
∴AC=AB+BC=25,
∵CD=10,AD=![]() ,
,
∴AC+CD=AD,
∴△ACD是直角三角形,∠ACD=90°,
∴∠ACB+∠DCM=90°,
∴∠ACB=∠CDM,
∵∠ABC=∠M=90°,
∴△ABC∽△CMD,
∴![]() ,
,
∴CM=2AB=6,DM=2BC=8,
∴BM=BC+CM=10,
∴BD=![]() =
=![]() ,故⑤正确;
,故⑤正确;
故答案为:②③④⑤.

练习册系列答案
相关题目