题目内容
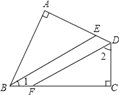
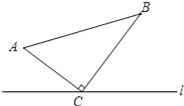
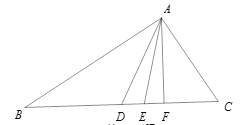
【题目】如图所示，三亚有三个车站A、B、C成三角形，一辆公共汽车从B站前往到C站。
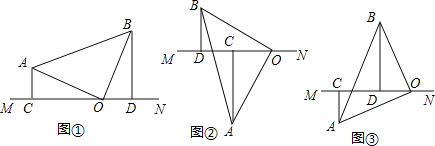
（1）当汽车运动到点D时，刚好BD=CD，连接AD，AD这条线段是什么线段？这样的线段在△ABC中有几条？此时有面积相等的三角形吗？
（2）汽车继续向前运动，当运动到点E时，发现∠BAE=∠CAE，那么AE这条线段是什么线段？在△ABC中，这样的线段又有几条？
（3）汽车继续向前运动，当运动到点F时，发现∠AFB=∠AFC=90°，则AF是什么线段？在△ABC中，这样的线段有几条？
【答案】（1）AD是△ABC中BC边上的中线，三角形中有三条中线．此时△ABD与△ADC的面积相等。
（2）AE是△ABC中∠BAC的角平分线，三角形中角平分线有三条。
（3）AF是△ABC中BC边上的高线，三角形有三条高线。
【解析】（1）由于BD=CD，则点D是BC的中点，AD是中线，三角形的中线把三角形分成两个面积相等的三角形；（2）由于∠BAE=∠CAE，由AE是三角形的角平分线；（3）由于∠AFB=∠AFC=90°，则AF是三角形的高线．
解：（1）AD是△ABC中BC边上的中线，三角形中有三条中线．此时△ABD与△ADC的面积相等．
（2）AE是△ABC中∠BAC的角平分线，三角形上角平分线有三条．
（3）AF是△ABC中BC边上的高线，高线有时在三角形外部，三角形中有三条高线．
“点睛”本题考查了三角形的高线、角平分线、中线的概念，它们分别都有三条．
亮点激活精编提优100分大试卷系列答案
【题目】某校1200名学生参加了全区组织的“经典诵读”活动，该校随机选取部分学生，对他们在三、四两个月的诵读时间进行调查，下面是根据调查数据制作的统计图表的一部分．
根据以上信息，解答下列问题：
（1）本次调查的学生数为__人；
（2）图表中的a、b、c的值分别为__，__，__；
（3）在被调查的学生中，四月份日人均诵读时间在1＜x≤1.5范围内的人数比三月份在此范围的人数多__人；
（4）试估计该校学生四月份人均诵读时间在1小时以上的人数．
四月日人均诵读时间的统计表
日人均诵读时间x/h | 人数 | 百分比 |
0≤x≤0.5 | 6 | |
0.5＜x≤1 | 30 | |
1＜x≤1.5 | 50% | |
1.5＜x≤2 | 10 | 10% |
2＜x≤2.5 | b | c |
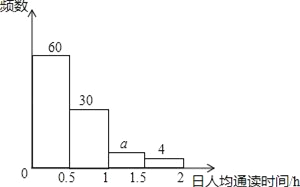
三月日人均诵读时间的频数分布直方图
