题目内容
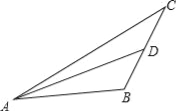
【题目】如图,在△ABC中(AB>BC),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长.
【答案】AC=48;AB=28
【解析】
试题分析:首先设BD=CD=x,AB=y,则AC=4x,然后分AC+CD=60,AB+BD=40和AC+CD=40,AB+BD=60两种情况分别求出x和y的值,然后看三角形的三边关系判定是否都符合条件.
试题解析:∵AD是BC边上的中线,AC=2BC, ∴BD=CD, 设BD=CD=x,AB=y,则AC=4x,
分为两种情况:①AC+CD=60,AB+BD=40, 则4x+x=60,x+y=40, 解得:x=12,y=28,
即AC=4x=48,AB=28;
②AC+CD=40,AB+BD=60, 则4x+x=40,x+y=60, 解得:x=8,y=52,
即AC=4x=32,AB=52,BC=2x=16, 此时不符合三角形三边关系定理;
综合上述:AC=48,AB=28.

练习册系列答案
相关题目