��Ŀ����
����Ŀ����ͼ����֪���κ���y=ax2��2ax+c��a��0����ͼ����x�Ḻ���ύ�ڵ�A����1��0������y�������ύ�ڵ�B������ΪP����OB=3OA��һ�κ���y=kx+b��ͼ��A��B��
��1����һ�κ�������ʽ��
��2����P�����ꣻ
��3��ƽ��ֱ��ABʹ�����P�������M��ƽ�ƺ��ֱ���ϣ��� ![]() �����M���ꣻ
�����M���ꣻ
��4���������ߵĶԳ��ύx���ڵ�E������AP��y���ڵ�D������Q��N�ֱ�Ϊ���߶�PE��PD�ϵĶ��㣬����QD��QN����ֱ��д��QD+QN����Сֵ��
���𰸡�
��1��
�⣺��A����1��0����
��OA=1
��OB=3OA��
��B��0��3��
��ͼ���A��B�����һ�κ����Ľ���ʽΪ��y=3x+3
��2��
�⣺�߶��κ���y=ax2��2ax+c��a��0����ͼ����x�Ḻ���ύ�ڵ�A����1��0������y�������ύ�ڵ�B��0��3����
��c=3��a=��1��
����κ����Ľ���ʽΪ��y=��x2+2x+3
��������y=��x2+2x+3�Ķ���P��1��4��
��3��
�⣺��ƽ�ƺ��ֱ�ߵĽ���ʽΪ��y=3x+m
��ֱ��y=3x+m��P��1��4����
��m=1��
��ƽ�ƺ��ֱ��Ϊy=3x+1
��M��ֱ��y=3x+1����
��M��x��3x+1��
�ٵ���M��x���Ϸ�ʱ���� ![]() ��
��
�� ![]() ��
��
�� ![]()
�ڵ���M��x���·�ʱ���� ![]() ��
��
�� ![]() ��
��
�� ![]() ��
�� ![]()
��4��
�⣺����D����ֱ��x=1�ĶԳƵ�D�䣬����D����D��N��PD�ڵ�N��
����x2+2x+3=0ʱ����ã�x=��1��x=3��
��A����1��0����
P��������1��4����
��ɵ�PD����ʽΪ��y=2x+2��
����ND���PD��
��ND�����ʽΪy=kx+b��
��k=�� ![]() ��
��
��D�䣨2��2�����뼴�����b��ֵ��
�ɵú�������ʽΪy=�� ![]() x+3��
x+3��
������������ʽ��ɷ�����ã� 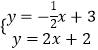 ��
��
��� 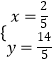 ��
��
��N�� ![]() ��
�� ![]() ����
����
�������ľ��빫ʽ��d= ![]() =
= ![]() ��
��
��������СֵΪ ![]()
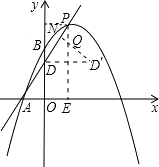
����������1�����������ߵĽ���ʽ���ɵó�B��0��3��������OB=3OA�������OA�ij���Ҳ�͵ó���A������꣬Ȼ��A��B���������ֱ��AB�Ľ���ʽ�У����ɵó�����2������1���ó���A��������������ߵĽ���ʽ�У������a��ֵ��Ҳ��ȷ���������ߵĽ���ʽ���������P������ꣻ��3�������ƽ�ƺ��ֱ�ߵĽ���ʽ���ɸ��ݴ˽���ʽ���M�����꣨������꣬����ֱ�ߵĽ���ʽ��ʾ�������꣩��Ȼ���M��x��Ĵ����费��ΪE���ڹ�����ֱ��������AME�У�����M��������ʾ��ME��AE�ij���Ȼ����ݡ�OAM������ֵ���M�����꣮������Ҫ��M��x���Ϸ���x���·����������⣮����һ��������4������D����ֱ��x=1�ĶԳƵ�D�䣬����D����D��N��PD�ڵ�N�����ݴ��߶�������QD+QN����Сֵ��
�����㾫�������ն��κ�����ͼ��Ͷ��κ����������ǽ����ĸ�������Ҫ֪�����κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�����Ŀ���л�������ԴԶ�������л����֣�Ԣ����㣬Ϊ�˴������㴫ͳ�Ļ���ijУ��ί��֯��һ��ȫУ3000��ѧ���μӵġ�������д�����������������в���ѧ���ijɼ���������50�֣�Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ������200��ѧ���ijɼ����ɼ�xȡ�������ܷ�100�֣���Ϊ���������������õ����в�������ͳ��ͼ����
�ɼ�x/�� | Ƶ�� | Ƶ�� |
50��x��60 | 10 | 0.05 |
��60��x��70 | 30 | 0.15 |
��70��x��80 | 40 | n |
��80��x��90 | m | 0.35 |
��90��x��100 | 50 | 0.25 |
�����������Ϣ������������⣺
��1��m= �� n=��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����α����ɼ�����λ�������������Σ�
��4�����ɼ���90�����ϣ�����90�֣���Ϊ���š��ȣ����У�μ���α�����3000��ѧ���гɼ����š���Լ�ж����ˣ�



