题目内容
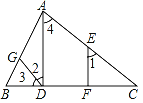
【题目】如图,已知∠ADC=∠EFC,∠3=∠C,可推得∠1=∠2.理由如下:
解:因为∠ADC=∠EFC(已知)
所以AD∥EF( ).
所以∠1=∠4( ),
因为∠3=∠C(已知),
所以AC∥DG( ).
所以∠2=∠4( ).
所以∠1=∠2(等量代换).

【答案】见解析.
【解析】
根据∠ADC=∠EFC,可得AD∥EF,利用同位角相等,两直线平行,
进而可得:∠1=∠4利用两直线平行,同位角相等,根据∠3=∠C可得:AC∥DG利用同位角相等,两直线平行,进而可得:∠2=∠4利用两直线平行,内错角相等,继而可得:∠1=∠2,利用等量代换.
解:因为∠ADC=∠EFC(已知),
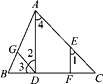
所以AD∥EF(同位角相等,两直线平行).
所以∠1=∠4(两直线平行,同位角相等).
因为∠3=∠C(已知),
所以AC∥DG(同位角相等,两直线平行).
所以∠2=∠4(两直线平行,内错角相等).
所以∠1=∠2(等量代换).

练习册系列答案
相关题目