题目内容
【题目】如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( ) 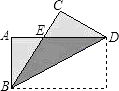
A.△EBD是等腰三角形,EB=ED
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形
【答案】B
【解析】解:∵ABCD为矩形 ∴∠A=∠C,AB=CD
∵∠AEB=∠CED
∴△AEB≌△CED(故D选项正确)
∴BE=DE(故A选项正确)
∠ABE=∠CDE(故B选项不正确)
∵△EBA≌△EDC,△EBD是等腰三角形
∴过E作BD边的中垂线,即是图形的对称轴.(故C选项正确)
故选:B.
【考点精析】利用矩形的性质和翻折变换(折叠问题)对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
相关题目
【题目】某校七年级学生开展踢毽子比赛活动,每班派5名同学参加,按团体总分多少排列名次,在规定的时间内每人踢100个以上(含100)为优秀.下表是甲班和乙班成绩最好的5名学生的比赛数据(单位:个)
1号 | 2号 | 3号 | 4号 | 5号 | 合计 | |
甲 | 100 | 98 | 110 | 89 | 103 | 500 |
乙 | 89 | 100 | 95 | 119 | 97 | 500 |
统计发现两班总分相等,S![]()
![]() S
S![]() , 此时有同学建议,可以通过考查数据中的其他信息作为参考,请你解答下列问题:
, 此时有同学建议,可以通过考查数据中的其他信息作为参考,请你解答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)根椐以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.