题目内容
【题目】如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为 _________ .

【答案】60°.
【解析】
试题分析:可证明△COD≌△COB,得出∠D=∠CBO,再根据∠BAC=80°,得∠BAD=100°,由角平分线可得∠BAO=40°,从而得出∠DAO=140°,根据AD=AO,可得出∠D=20°,即可得出∠CBO=20°,则∠ABC=40°,最后算出∠BCA=60°
试题解析:∵△ABC三个内角的平分线交于点O,
∴∠ACO=∠BCO,
在△COD和△COB中,
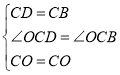 ,
,
∴△COD≌△COB,
∴∠D=∠CBO,
∵∠BAC=80°,
∴∠BAD=100°,
∴∠BAO=40°,
∴∠DAO=140°,
∵AD=AO,
∴∠D=20°,
∴∠CBO=20°,
∴∠ABC=40°,
∴∠BCA=60°.

练习册系列答案
相关题目


