题目内容
【题目】在平面直角坐标系中,已知点A(a,0),B (b,0),a、b满足方程组![]() ,C为y轴正半轴上一点,且
,C为y轴正半轴上一点,且![]() .
.
(1)求A、B、C三点的坐标;
(2)是否存在点D(t,-t)使![]() ?若存在,请求出D点坐标;若不存在,请说明理由.
?若存在,请求出D点坐标;若不存在,请说明理由.
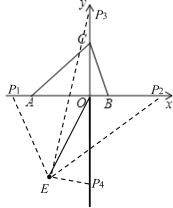
(3)已知E(-2,-4),若坐标轴上存在一点P,使![]() ,请求出P的坐标.
,请求出P的坐标.

【答案】(1)A(-3,0),B(1,0),C(0,3);(2)D(1,-1)或(-1,1);(3)P(3,0)或(-3,0)或(0,6)或(0,-6).
【解析】
(1)解出方程组即可得到点A,B的坐标,利用S△ABC=6,求出点C的坐标;
(2)利用![]() 求出点D的坐标即可;
求出点D的坐标即可;
(3)设点P(m,0),分点P在x轴和在y轴两种情况讨论,结合点E坐标和△ABC的面积分别求出点P坐标.
解:(1)方程组![]() ,解得:
,解得:![]() ,
,
∴A(-3,0),B(1,0),
∵c为y轴正半轴上一点,且S△ABC=6,
∴![]() AB×OC=6,解得OC=3,
AB×OC=6,解得OC=3,
∴C(0,3);
(2)∵D(t,-t),且S△PAB=![]() S△ABC,
S△ABC,
∴![]() ×4×|t|=
×4×|t|=![]() ×6,解得t=±1,
×6,解得t=±1,
∴D(1,-1)或(-1, 1);
(3)如图,∵![]() ,E(-2,-4),设点P坐标为(m,0),
,E(-2,-4),设点P坐标为(m,0),
当点P在x轴上时,
![]() ,
,
解得m=±3,
∴点P的坐标为(3,0)或(-3,0);
当点P在y轴上时,
![]() ,
,
解得m=±6,
∴点P的坐标为(0,6)或(0,-6);
综上:坐标轴上存在点P,坐标为(3,0)或(-3,0)或(0,6)或(0,-6);

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目