题目内容

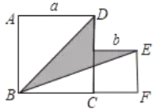
【题目】如图，两个正方形边长分别为a、b，且满足a b 10， ab 12，图中阴影部分的面积为（ ）

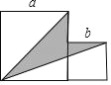
A.100B.32C.144D.36

【答案】B

【解析】

将a＋b＝10两边平方，利用完全平方公式展开，将ab的值代入求出a2＋b2的值，即为两正方形的面积之和；由两个正方形的面积减去两个直角三角形的性质即可求出阴影部分面积．

解：如图所示，将a＋b＝10两边平方得：（a＋b）2＝a2＋b2＋2ab＝100，
将ab＝12代入得：a2＋b2＋24＝100，即a2＋b2＝76，
则两个正方形面积之和为76；
∴S阴影＝S两正方形S△ABDS△BEF＝a2＋b2a2b(a＋b)＝(a2＋b2ab)＝×(7612)＝32，

故答案为：B．

练习册系列答案
相关题目

【题目】如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB的中点，

（1）求证：AC2=ABAD；

（2）求证：CE∥AD；

（3）若AD=4，AB=6，求 的值．

【题目】夹在两条平行线间的正方形ABCD、等边三角形DEF如图所示，顶点A、F分别在两条平行线上．若A、D、F在一条直线上，则∠1与∠2的数量关系是（　　）

A. ∠1+∠2=60° B. ∠2﹣∠1=30° C. ∠1=2∠2． D. ∠1+2∠2=90°

【题目】某开发商的经适房的三个居民小区A、B、C在同一条直线上，位置如图所示．其中小区B到小区A、C的距离分别是70m和150m，现在想在小区A、C之间建立一个超市，要求各小区居民到超市总路程的和最小，那么超市的位置应建在（　　）

A.小区AB.小区BC.小区CD.AC的中点

【题目】沿图1长方形中的虚线平均分成四块小长方形,然后按图2的形状拼成一个正方形.

(1)图2中的阴影部分的面积为 .

(2)观察图2，请你写出代数式(m+n)2、(m-n)2、mn之间的等量关系式.

(3)根据你得到的关系式解答下列问题：若x+y=-6,xy=5,则x–y= .

(4)实际上有许多代数恒等式可以用图形的面积来表示.如图3,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.

【题目】如图，已知四边形ABCD是平行四边形，下列结论中不正确的是(　　)

A. 当AB＝BC时，它是菱形 B. 当AC⊥BD时，它是菱形

C. 当∠ABC＝90°时，它是矩形 D. 当AC＝BD时，它是正方形

【题目】在一次数学课上，张老师出示了一个题目：“如图，ABCD的对角线相交于点O，过点O作EF垂直于BD交AB，CD分别于点F，E，连接DF，BE．请根据上述条件，写出一个正确结论．”其中四位同学写出的结论如下：

小青：OE=OF；小何：四边形DFBE是正方形；

小夏：S四边形AFED=S四边形FBCE；小雨：∠ACE=∠CAF．

这四位同学写出的结论中不正确的是（　　）

A. 小青 B. 小何 C. 小夏 D. 小雨

【题目】在平面直角坐标系中，已知点A（0，2），B（4，0），C（4，3）三点．

（1）建立平面直角坐标系并描出A、B、C三点

（2）求△ABC的面积；

（3）如果在第二象限内有一点P（m，1），且四边形ABOP的面积是△ABC的面积的两倍；求满足条件的P点坐标．

【题目】在平面直角坐标系中，已知点A（a，0），B (b，0)，a、b满足方程组，C为y轴正半轴上一点，且．

（1）求A、B、C三点的坐标；

（2）是否存在点D（t，-t）使？若存在，请求出D点坐标；若不存在，请说明理由．

（3）已知E(-2，-4)，若坐标轴上存在一点P，使，请求出P的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网