题目内容
【题目】如图，海上有A、B、C三座小岛，小岛B在岛A的正北方向，距离为121海里，小岛C分别位于岛B的南偏东53°方向，位于岛A的北偏东27°方向，求小岛B和小岛C之间的距离.（参考数据：sin27°≈
，cos27°≈
，tan27°≈
，sin53°≈
，cos53°≈
，tan53°≈
）
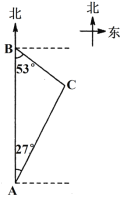
【答案】小岛B和小岛C之间的距离55海里.
【解析】
先过点C作CD⊥AB，垂足为点D，设BD=x海里，得出AD=（121-x）海里，在Rt△BCD中，根据
，求出CD，再根据
，求出BD，在Rt△BCD中，根据
，求出BC，从而得出答案．
解：根据题意可得，在△ABC中，AB=121海里，∠ABC=53°，∠BAC=27°，
过点C作CD⊥AB，垂足为点D．
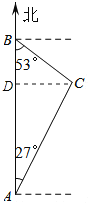
设BD=x海里，则AD=（121-x）海里，
在Rt△BCD中，
则
CD=xtan53°≈
在Rt△ACD中，则CD=ADtan27°≈
则
解得，x=33，
即BD=33．
在Rt△BCD中，
则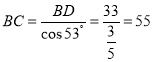
答：小岛B和小岛C之间的距离约为55海里.
练习册系列答案
相关题目
