题目内容
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上的一个动点,作
上的一个动点,作![]() ,
,![]() 交射线
交射线![]() 于点
于点![]() ,射线
,射线![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
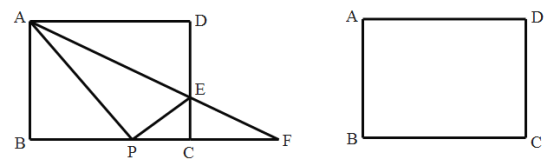
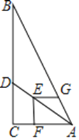
(1)如图,当![]() 在边
在边![]() 上时(点
上时(点![]() 与点
与点![]() 、
、![]() 都不重合),求
都不重合),求![]() 关于
关于![]() 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;
(2)当![]() 时,求
时,求![]() 的长;
的长;
(3)当![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)![]() ;(2)3;(3)3或7.
;(2)3;(3)3或7.
【解析】
(1)P在BC上运动时,要求y关于x的函数解析式,只需要用勾股定理表示PE2=PC2+EC2就可以使问题到解决,而关键是解决PE2,又在Rt△APE中由勾股定理求得,从而解决问题;(2)把x=3的值代入第一问的解析式就可以求出CE的值,再利用三角形相似就可以求出CF的值;(3)由条件可以证明△ABP∽△PCE,可以得到![]() =2,再分情况讨论,从而求出BP的值.
=2,再分情况讨论,从而求出BP的值.
解:(1)如图:
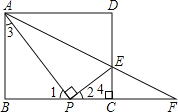
∵四边形ABCD是矩形,
∴AB=CD=4,BC=AD=5,∠B=∠BCD=∠D=90°,
∵BP=x,CE=y,
∴PC=5-x,DE=4-y,
∵AP⊥PE,
∴∠APE=90°,∠1+∠2=90°,
∵∠1+∠3=90°,
∴∠2=∠3,
∴△ABP∽△PCE,
∴![]()
∴![]()
∴![]() ;
;
(2)当x=3时,![]() ,
,
即CE=![]() ,
,
∴DE=![]() ,
,
∵四边形ABCD是矩形,
∴AD∥BF.
∴△AED∽△FEC,
∴![]() ,
,
∴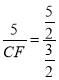 ,
,
∴CF=3;
(3)根据tan∠PAE=![]() ,可得:
,可得:![]() =2
=2
由(1)可知,当点P在边BC上时:△ABP∽△PCE
∴![]() =2
=2
于是:![]()
解得:x=3,y=1.5
如图,当点P在BC的延长线上时,
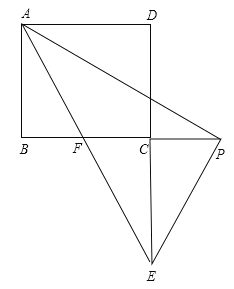
同理可证:△ABP∽△PCE
此时,BP=x-5
∴![]()
解得:x=7,y=3.5.
p>∴BP=3或7.
练习册系列答案
相关题目