��Ŀ����
����Ŀ����ABC�ǵ���ֱ�������Σ�AC��BC����ACB��90��
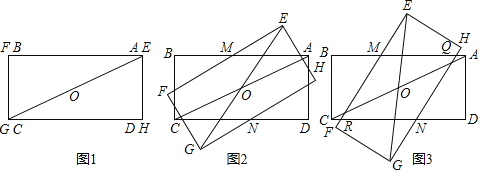
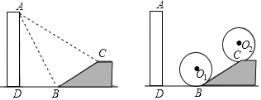
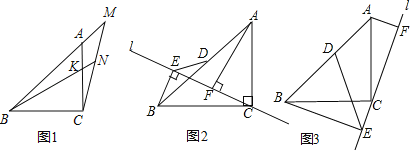
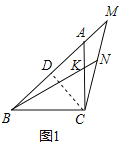
��1����ͼ1����M��BA�ӳ�����һ�㣬����CM��K��AC��һ�㣬BK�ӳ��߽�CM��N����MBN����MCA��15����BK��8����CM�ij��ȣ�
��2����ͼ2��ֱ��l������C��AF��l�ڵ�F��BE��l�ڵ�E����D��AB���е㣬����ED����֤��AF��BE+![]() DE��
DE��
��3����ͼ2�е�ֱ��l��ת����ABC���ⲿ�������������䣬�����AF��BE��DE�Ĺ�ϵ����д����Ҫ�IJ��裮
���𰸡���1��4![]() ����2��AF=BE+
����2��AF=BE+![]() DE������������3��AF+BE��
DE������������3��AF+BE��![]() DE��������
DE��������
��������
��1����C��CD��AB��D���ɵ���ֱ�������ε����ʿɵ���ABC����BAC��45��������ȷ����KBC��30��������ֱ�������ε����ʵõ�BC��4![]() �����CD��
�����CD��![]() BC��2
BC��2![]() ����ֱ�������μ��ɵõ����ۣ�
����ֱ�������μ��ɵõ����ۣ�
��2����ͼ2������DF��CD�����ݵ���ֱ�������ε����ʵõ�CD��BD����CDB��90������ȫ�������ε����ʵõ�BE��CF��CE��AF���Ƴ���BDE�ա�CDF������ȫ�������ε����ʵõ���EDB����FDC��DE��DF��������ǵ����ʵõ���EDF��90�������ݵ���ֱ�������ε����ʵõ�EF��![]() DE�����ǵõ����ۣ�
DE�����ǵõ����ۣ�
��3�����ۣ�BE+AF��![]() DE������CD��DF���ɣ�2��֤����BCE�ա�ACF������ȫ�������ε����ʵõ�BE��CF��CE��AF���ɣ�2��֤����DEF�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʵõ�EF��
DE������CD��DF���ɣ�2��֤����BCE�ա�ACF������ȫ�������ε����ʵõ�BE��CF��CE��AF���ɣ�2��֤����DEF�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʵõ�EF��![]() DE�����ɵõ����ۣ�
DE�����ɵõ����ۣ�
�⣺��1����C��CD��AB��D��
��AC��BC����ACB��90����
���ABC����BAC��45����
�ߡ�MBN��15����
���KBC��30����
��BK��8��
��BC��4![]() ��
��
��CD��![]() BC��2
BC��2![]()
�ߡ�MCA��15������BAC��45����
���M��30����
��CM��2CD��4![]() ��
��
��2����BE��CE��
���BEC����ACB��90����
���EBC+��BCE����BCE+��ACF��90����
���EBC����ACF��
��AF��l�ڵ�F��
���AFC��90����
����BCE����ACF��
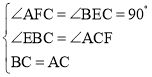 ��
��
���ACF�ա�CBE��AAS����
��ͼ2������DF��CD��
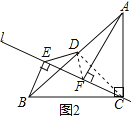
����D��AB���е㣬
��CD��BD����CDB��90����
�ߡ�ACF�ա�CBE��
��BE��CF��CE��AF��
�ߡ�EBD����DCF��
����BDE����CDF��
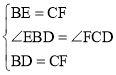 ��
��
���BDE�ա�CDF��SAS����
���EDB����FDC��DE��DF��
�ߡ�CDF+��FDB��90������EDB+��BDF��90����
���EDF��90����
���EDF�ǵ���ֱ�������Σ�
��EF��![]() DE��
DE��
��AF��CE��EF+CF��BE+![]() DE��
DE��
��3����ͼ3������CD��DF��
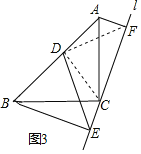
�ɣ�2��֤����BCE�ա�ACF��
��BE��CF��CE��AF��
�ɣ�2��֤����DEF�ǵ���ֱ�������Σ�
��EF��![]() DE��
DE��
��EF��CE+CF��AF+BE��![]() DE��
DE��
��AF+BE��![]() DE��
DE��