��Ŀ����
����Ŀ��������⣺��ͼ1�������ǰ����������ABCD�ϣ�ʹ���ǰ��ֱ�Ƕ���P�ڶԽ���AC�ϣ�һ��ֱ�DZ߾�����B����һ��ֱ�DZ߽���DC���E����֤��PB=PE
�������⣺ѧ���ף���ͼ1������P��PM��BC��PN��CD������ֱ�ΪM��Nͨ��֤����������ȫ�ȣ�����֤�������߶���ȣ�
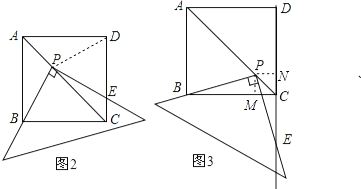
ѧ���ң�����DP����ͼ2��������֤��PD=PB��Ȼ����ͨ�����ȽǶԵȱߡ�֤��PE=PD���Ϳ���֤��PB=PE�ˣ�
������⣺����ѡ������һ�ַ�������֤����
�������죺��ͼ3���ƶ����ǰ壬ʹ���ǰ��ֱ�Ƕ���P�ڶԽ���AC�ϣ�һ��ֱ�DZ߾�����B����һ��ֱ�DZ߽�DC���ӳ����ڵ�E��PB=PE������������������֤����������������˵�����ɣ�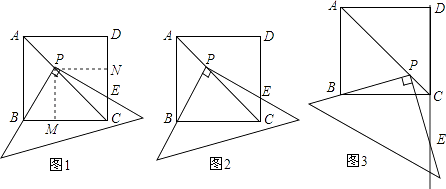
���𰸡�֤������ͼ1��
���ı���ABCDΪ�����Σ�
���BCD=90�㣬ACƽ�֡�BCD��
��PM��BC��PN��CD��
���ı�PMCNΪ���Σ�PM=PN��
�ߡ�BPE=90�㣬��BCD=90�㣬
���PBC+��CEP=180�㣬
����CEP+��PEN=180�㣬
���PBM=��PEN��
�ڡ�PBM�͡�PEN��
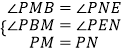
���PBM�ա�PEN��AAS����
��PB=PE��
��ͼ2������PD��
���ı���ABCDΪ�����Σ�
��CB=CD��CAƽ�֡�BCD��
���BCP=��DCP��
�ڡ�CBP�͡�CDP��
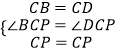 ��
��
���CBP�ա�CDP��SAS����
��PB=PD����CBP=��CDP��
�ߡ�BPE=90�㣬��BCD=90�㣬
���PBC+��CEP=180�㣬
����CEP+��PEN=180�㣬
���PBC=��PED��
���PED=��PDE��
��PD=PE��
��PB=PD��
��ͼ3��PB=PE��������
�������£�����P��PM��BC��PN��CD������ֱ�ΪM��N��
���ı���ABCDΪ�����Σ�
���BCD=90�㣬ACƽ�֡�BCD��
��PM��BC��PN��CD��
���ı�PMCNΪ���Σ�PM=PN��
���MPN=90�㣬
�ߡ�BPE=90�㣬��BCD=90�㣬
���BPM+��MPE=90�㣬
����MEP+��EPN=90�㣬
���BPM=��EPN��
�ڡ�PBM�͡�PEN��
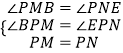 ��
��
���PBM�ա�PEN��AAS����
��PB=PE��
������������ͼ1�����������ε����ʵá�BCD=90�㣬ACƽ�֡�BCD����PM��BC��PN��CD�����ı�PMCNΪ���Σ����ݽ�ƽ�������ʵ�PM=PN�������ı����ڽǺ͵õ���PBC+��CEP=180�㣬�����õȽǵIJ�����ȵõ���PBM=��PEN��Ȼ����ݡ�AAS��֤����PBM�ա�PEN����PB=PE��
����ͼ2������PD�����������ε����ʵ�CB=CD��CAƽ�֡�BCD�����ݽ�ƽ���ߵ����ʵá�BCP=��DCP���ٸ��ݡ�SAS��֤����CBP�ա�CDP����PB=PD����CBP=��CDP�������ı����ڽǺ͵õ���PBC+��CEP=180�㣬�����õȽǵIJ�����ȵõ���PBC=��PED�����PED=��PDE������PD=PE�����ǵõ�PB=PD��
����ͼ3������P��PM��BC��PN��CD������ֱ�ΪM��N�����������ε����ʵá�BCD=90�㣬ACƽ�֡�BCD����PM��BC��PN��CD���õ��ı�PMCNΪ���Σ�PM=PN�����MPN=90�㣬���õȽǵ������ȵõ���BPM=��EPN��Ȼ����ݡ�AAS��֤����PBM�ա�PEN������PB=PE��

 �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
