题目内容
【题目】（1）（探索发现）
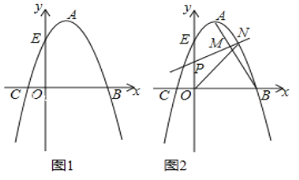
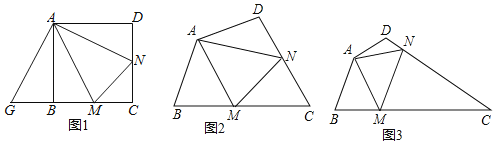
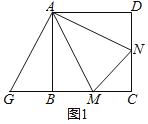
如图1，在正方形ABCD中，点M，N分别是边BC，CD上的点，∠MAN＝45°，若将△DAN绕点A顺时针旋转90°到△BAG位置，可得△MAN≌△MAG，若△MCN的周长为8，则正方形ABCD的边长为 ．
（2）（类比延伸）
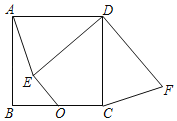
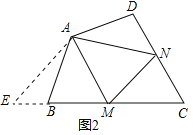
如图2，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B+∠D＝180°，点M，N分别在边BC，CD上的点，∠MAN＝60°，请判断线段BM，DN，MN之间的数量关系，并说明理由．
（3）（拓展应用）
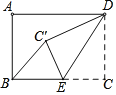
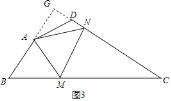
如图3，在四边形ABCD中，AB＝AD＝2，∠ADC＝120°，点M，N分别在边BC，CD上，连接AM，MN，AN，△ABM是等边三角形，AM⊥AD于点A，∠DAN＝15°，请直接写出△CMN的周长．
【答案】（1）4；（2）MN＝NM+DN，理由见解析；（3）6+4
【解析】
（1）求出MN＝BM+DN，证明△MNC的周长＝BC+CD即可解决问题；
（2）延长CB至E，使BE＝DN，连接AE，首先证明△ABE≌△ADN，然后证明△MAN≌△MAE，根据全等三角形的性质可得结论；
（3）如图3，延长BA，CD交于G，解30度直角三角形求出DG和AG，进而得到BC和CD，然后根据（2）中结论计算即可．
解：（1）如图1中，∵△MAN≌△MAG，
∴MN＝GM，
∵DN＝BG，GM＝BG+BM，
∴MN＝BM+DN，
∵△CMN的周长为：MN+CM+CN＝8，
∴BM+CM+CN+DN＝8，
∴BC+CD＝8，
∴BC＝CD＝4，
故答案为4；
（2）结论：MN＝NM+DN．
理由：如图2中，延长CB至E，使BE＝DN，连接AE，
∵∠ABC+∠D＝180°，∠ABC+∠ABE＝180°，
∴∠D＝∠ABE，
在△ABE和△ADN中，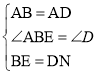
，
∴△ABE≌△ADN（SAS），
∴AN＝AE，∠DAN＝∠BAE，
∵∠BAD＝2∠MAN，
∴∠DAN+∠BAM＝∠MAN，
∴∠MAN＝∠EAM，
在△MAN和△MAE中，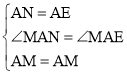
，
∴△MAN≌△MAE（SAS），
∴MN＝EM＝BE+BM＝BM+DN；
（3）如图3，延长BA，CD交于G，
∵∠BAM＝60°，∠MAD＝90°，
∴∠BAD＝150°，
∴∠GAD＝30°，
∵AD＝2，
∴DG＝1，AG＝，
∵∠DAN＝15°，
∴∠GAN＝45°，
∴AG＝GN＝，
∴BG＝2+，
∴BC＝2BG＝4+2，CG＝BG＝2+3，
∴CD＝CG﹣DG＝2+2，
由（2）得，MN＝BM+DN，
∴△CMN的周长＝CM+CN+MN＝CN+DN+CM+BM＝BC+CD＝4+2+2+2＝6+4．
