题目内容
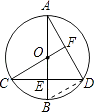
【题目】在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数. 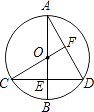
【答案】解:方法一:连接BD.
∵AB是⊙O直径,
∴BD⊥AD.
又∵CF⊥AD,
∴BD∥CF,
∴∠BDC=∠C.
又∵∠BDC= ![]() ∠BOC,
∠BOC,
∴∠C= ![]() ∠BOC.
∠BOC.
∵AB⊥CD,
∴∠C=30°,
∴∠ADC=60°.
方法二:设∠D=x,
∵CF⊥AD,AB⊥CD,∠A=∠A,
∴△AFO∽△AED,
∴∠D=∠AOF=x,
∴∠AOC=2∠ADC=2x,
∴x+2x=180,
∴x=60,
∴∠ADC=60°.

【解析】连接BD,根据平行线的性质可得:BD∥CF,则∠BDC=∠C,根据圆周角定理可得∠BDC= ![]() ∠BOC,则∠C=
∠BOC,则∠C= ![]() ∠BOC,根据直角三角形的两个锐角互余即可求解.
∠BOC,根据直角三角形的两个锐角互余即可求解.
【考点精析】通过灵活运用垂径定理,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧即可以解答此题.

练习册系列答案
相关题目
【题目】小洋八年级下学期的数学成绩(单位:分)如下表所示:
测试 类别 | 平时 | 期中 考试 | 期末 考试 | |||
测验1 | 测验2 | 测验3 | 测验4 | |||
成绩 | 106 | 102 | 115 | 109 | 112 | 110 |
(1)计算小洋该学期的数学平时平均成绩;
(2)如果该学期的总评成绩是根据如图所示的权重计算的,请计算出小洋该学期的数学总评成绩.