题目内容
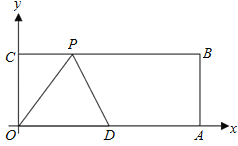
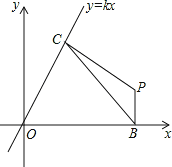
【题目】如图,已知平面直角坐标系中,直线y=kx(k≠0)经过点(a,![]() a)(a>0).线段BC的两个端点分别在x轴与直线y=kx上(B、C均与原点O不重合)滑动,且BC=2,分别作BP⊥x轴,CP⊥直线y=kx,交点为P,经探究在整个滑动过程中,P、O两点间的距离为定值 .
a)(a>0).线段BC的两个端点分别在x轴与直线y=kx上(B、C均与原点O不重合)滑动,且BC=2,分别作BP⊥x轴,CP⊥直线y=kx,交点为P,经探究在整个滑动过程中,P、O两点间的距离为定值 .
【答案】![]() .
.
【解析】
试题解析:∵直线y=kx(k≠0)经过点(a,![]() a),
a),
∴tan∠COB=![]() ,
,
∴∠COB=60°,
过点C作CE⊥x轴于点E,延长CP交x轴于点F,连接OP,如图,
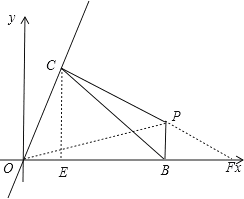
则∠OCE=∠CFE=30°,
设P点坐标为(x,y)(不妨设点P在第一象限,其他同理可求得),则OB=x,PB=y,
在Rt△PBF中,可得BF=![]() y,
y,
∴OF=OB+BF=x+![]() y,
y,
在Rt△OCF中,OC=![]() OF=
OF=![]() ,
,
在Rt△OCE中,OE=![]() OC=
OC=![]() ,
,
则CE=![]() OE=
OE=![]() ,BE=OB-OE=x-
,BE=OB-OE=x-![]() =
=![]() ,
,
在Rt△BCE中,由勾股定理可得CE2+BE2=BC2,
∴(![]() )2+(
)2+(![]() )2=22,
)2=22,
整理可求得x2+y2=![]() ,
,
∴OP=![]() ,
,
即O、P两点的距离为定值![]()

练习册系列答案
相关题目