Question

【题目】如图，在 Rt△ABC 中，∠BAC＝90°，∠BAC 的平分线交 BC 于点 O，以 O 为圆心作圆，⊙O 与 AC 相切于点 D．

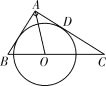
（1）试判断 AB 与⊙O 的位置关系，并加以证明；

（2）在 Rt△ABC 中，若 AC＝6，AB＝3，求切线 AD 的长．

Answer 1

【答案】（1）BA与⊙O相切，证明见解析；（2）AD的长为2.

【解析】

（1）过点O作OE⊥AB，垂足为E，连接OD，根据角平分线性质得出OE=OD，据此进一步证明即可.

（2）设⊙O的半径为r，根据△ABC面积=△AOC面积+△BOA面积进一步分析得出⊙O半径，然后通过证明AD=OD求出长度即可.

（1）

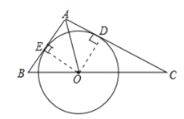
如图，过点O作OE⊥AB，垂足为E，连接OD，

∵AC是圆的切线，

∴OD⊥AC，

∵OA为∠BAC的角平分线，OE⊥AB，

∴OE=OD，

即OE是该圆的半径，

∴BA与⊙O相切；

（2）设⊙O的半径为r，

∵△ABC面积=△AOC面积+△BOA面积，

∴，

∵OE=OD=r，AC=6，AB=3，

∴，

即：，

∴，

∵OA为∠BAC的角平分线，

∴∠OAD=45°，

∵OD⊥AC，

∴∠AOD=45°，

∴AD=OD=r，

即AD的长为2.