题目内容
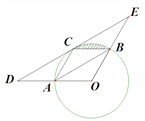
【题目】如图,□AOBC的顶点A、B、C在⊙O上,过点C作DE∥AB交OA延长线于D点,交OB延长线于点E .
(1)求证:CE是⊙O的切线;
(2)若OA=1,求阴影部分面积.
【答案】(1)证明见解析;(2)S阴影=![]()
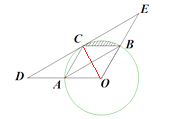
【解析】试题分析:连接OC,由垂径定理可知OC⊥AB,又DE∥AB,故OC⊥DE,因此可得CE是⊙O的切线;
(2)根据题意知ΔCOB是等边三角形,分别求出S扇形COB和SΔCOB,相减即可求解.
试题解析:(1)连接OC,如图,
∵四边形AOBC是平行四边形,
又OA=OB
∴平行四边形AOBC是菱形
∴OC⊥AB
∵DE∥AB,
∴OC⊥DE
∴CE是⊙O的切线;
(2)∵四边形AOBC是菱形
∴AO=BO=OC=CA
又OC=OB
∴ΔCOB是等边三角形
∴∠COB=60°,
∴SΔCOB=![]()
S扇形COB=![]()
故S阴影= S扇形COB- SΔCOB=![]()

练习册系列答案
相关题目