题目内容
【题目】如图,△ABC中,AB=AC,∠BAC=90°, 
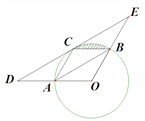
(1)CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,BE的延长线交CA的延长线于M,补全图形,并探究BE和CD的数量关系,并说明理由;
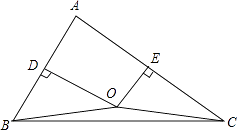
(2)若BC上有一动点P,且∠BPQ= ![]() ∠ACB,BQ⊥PQ于Q,PQ交AB于F,试探究BQ和PF之间的数量关系,并证明你的结论.
∠ACB,BQ⊥PQ于Q,PQ交AB于F,试探究BQ和PF之间的数量关系,并证明你的结论.
【答案】
(1)解:如图1,BE= ![]() CD,理由是:
CD,理由是:
∵BE⊥CD,
∴∠BEC=90°,
∵∠BAC=90°,
∴∠BEC=∠BAC,
∵∠EDB=∠ADC,
∴∠ABM=∠ACD,
∵AB=AC,∠BAM=∠BAC=90°,
∴△ABM≌△ACD,
∴CD=BM,
∵∠MCE=∠BCE,EC=EC,∠BEC=∠MEC=90°,
∴△MEC≌△BEC,
∴BE=EM,
∴BE= ![]() BM=
BM= ![]() CD
CD

(2)解:如图2,BQ= ![]() PF,理由是:
PF,理由是:
作∠ACB的平分线,交BQ延长线于E,交AB于D,
由(1)得:BE= ![]() CD,
CD,
∵∠BPQ= ![]() ∠ACB,∠BCE=
∠ACB,∠BCE= ![]() ∠ACB,
∠ACB,
∴∠BPQ=∠BCE,
∴PQ∥CE,
∴ ![]() =
= ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴BQ= ![]() PF
PF

【解析】(1)如图1,证明△ABM≌△ACD,得CD=BM,再证明△MEC≌△BEC,得BE=EM,则BE= ![]() CD;(2)如图2,根据(1)作辅助线,证明PQ∥EC,得
CD;(2)如图2,根据(1)作辅助线,证明PQ∥EC,得 ![]() ,利用(1)的结论BE=
,利用(1)的结论BE= ![]() CD,得BQ=
CD,得BQ= ![]() PF.
PF.
【考点精析】利用等腰直角三角形对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.

练习册系列答案
相关题目