题目内容
【题目】如图1所示，从边长为a的正方形纸片中剪去一个边长为b的小正方形，再沿着线段AB剪开，把剪成的两张纸拼成如图2的等腰梯形，
（1）设图1中阴影部分面积为S1 ， 图2中阴影部分面积为S2 ， 请直接用含a、b的代数式表示S1和S2；
（2）请写出上述过程所揭示的乘法公式．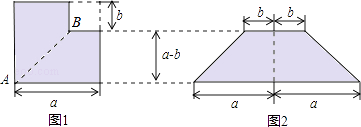 
【答案】
（1）解：∵大正方形的边长为a，小正方形的边长为b，
∴S1=a2﹣b2，
S2= 
（2a+2b）（a﹣b）=（a+b）（a﹣b）
（2）解：根据题意得：
（a+b）（a﹣b）=a2﹣b2
【解析】（1）先用大正方形的面积减去小正方形的面积，即可求出S1 ， 再根据梯形的面积公式即可求出S2 ． （2）根据（1）得出的值，直接可写出乘法公式（a+b）（a﹣b）=a2﹣b2 ．
练习册系列答案
寒假学与练系列答案
相关题目
