题目内容
如图，⊙O的半径为5，弦AB的长为6，M是弦AB 上的动点，则OM长的最小值为
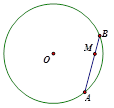
| A．5 | B．4 | C．3 | D．2 |
C.
试题分析：过O作OM⊥AB于M，此时线段OM的长最短，连接OA，根据垂径定理求出AM，根据勾股定理求出OM即可．
过O作OM⊥AB于M，此时线段OM的长最短，连接OA，
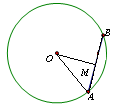
∵OM过O，OM⊥AB，
∴AM=
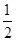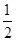AB=×8=4，在Rt△AMO中，由勾股定理得：OM=
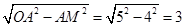，故选C．
考点: 1.垂径定理；2.勾股定理．
练习册系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
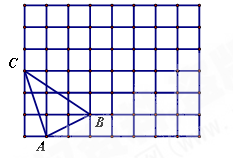
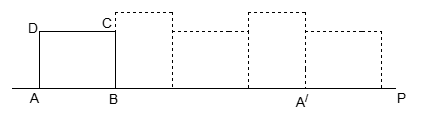
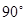，画出旋转后的△A1B2C2；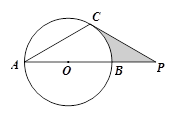
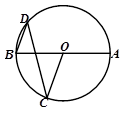
中，∠
，点
在
上，以
长为半径的圆与
分别交于点
，且∠
．判断直线
与
的位置关系，并证明你的结论.
π C．2π D．4π