题目内容
【题目】如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①△FPD是等腰直角三角形;②AP=EF;
③AD=PD;④∠PFE=∠BAP.其中,所有正确的结论是( )
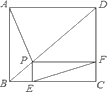
A. ①② B. ①④ C. ①②④ D. ①③④
【答案】C
【解析】如图,

∵P为正方形ABCD的对角线BD上任一点,
∴PA=PC,∠C=90°,
∵过点P作PE⊥BC于点E,PF⊥CD,
∴∠PEC=∠DFP=∠PFC=∠C=90°,
∴四边形PECF是矩形,
∴PC=EF,
∴PA=EF,故②正确,
∵BD是正方形ABCD的对角线,
∴∠ABD=∠BDC=∠DBC=45°,
∵∠PFC=∠C=90°,
∴PF∥BC,
∴∠DPF=45°,
∵∠DFP=90°,
∴△FPD是等腰直角三角形,故①正确,
在△PAB和△PCB中,
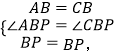 ,
,
∴△PAB≌△PCB,
∴∠BAP=∠BCP,
在矩形PECF中,∠PFE=∠FPC=∠BCP,
∴∠PFE=∠BAP.故④正确,
∵点P是正方形对角线BD上任意一点,
∴AD不一定等于PD,
只有∠BAP=22.5°时,AD=PD,故③错误,
故选C

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目