��Ŀ����
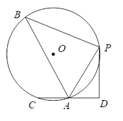
����Ŀ����ͼ��A��B���������ֱ��ǣ�8��0������0��6������P�ɵ�B������BA�������A������ֱ���˶����ٶ�Ϊÿ��3����λ���ȣ���Q��A������AO��OΪ����ԭ�㣩�������O������ֱ���˶����ٶ�Ϊÿ��2����λ���ȣ�����PQ�������˶�ʱ��Ϊt��0��t��![]() ���룮����������⣺
���룮����������⣺
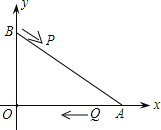
��1����tΪ��ֵʱ��PQ��BO��
��2������AQP�����ΪS��
����S��t֮��ĺ�����ϵʽ�������S�����ֵ��
�������ǹ涨����P��Q������ֱ�Ϊ��x1��y1������x2��y2�����������꣨x2��x1��y2��y1����Ϊ������PQ�������꣮��Sȡ���ֵʱ��������PQ�������꣮
���𰸡���1����t=![]() ��ʱ��PQ��BO��2����S=
��ʱ��PQ��BO��2����S=![]() ��0��t��
��0��t��![]() ����5����
����5����![]() ����3��
����3��
���������⣺��1����A��B���������ֱ��ǣ�8��0������0��6������OB=6��OA=8��
��![]() ��
��
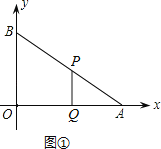
��ͼ������PQ��BOʱ��AQ=2t��BP=3t����AP=10��3t��
��PQ��BO����![]() ����
����![]() �����t=
�����t=![]() ��
��
����t=![]() ��ʱ��PQ��BO��
��ʱ��PQ��BO��
��2���ɣ�1��֪��OA=8��OB=6��AB=10��
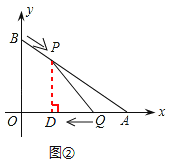
����ͼ����ʾ������P��PD��x���ڵ�D��
��PD��BO��
����APD�ס�ABO��
��![]() ����
����![]() �����PD=6��
�����PD=6��![]() t��
t��
��![]() ��
��
��S��t֮��ĺ�����ϵʽΪ��S=![]() ��0��t��
��0��t��![]() ����
����
����t=![]() ��ʱ��Sȡ�����ֵ�����ֵΪ5��ƽ����λ����
��ʱ��Sȡ�����ֵ�����ֵΪ5��ƽ����λ����
����ͼ����ʾ����Sȡ���ֵʱ��t=![]() ��
��
��PD=6��![]() t=3����PD=
t=3����PD=![]() BO��
BO��
��PD��BO������ʱPDΪ��OAB����λ�ߣ���OD=![]() OA=4����P��4��3����
OA=4����P��4��3����
��AQ=2t=![]() ����OQ=OA��AQ=
����OQ=OA��AQ=![]() ����Q��
����Q��![]() ��0����
��0����
�����⣬������PQ��������Ϊ��![]() ��4��0��3��������
��4��0��3��������![]() ����3����
����3����
����Sȡ���ֵʱ��������PQ��������Ϊ��![]() ����3����
����3����
��1����ͼ����ʾ����PQ��BOʱ������ƽ���߷��߶γɱ������������߶α���ʽ![]() �����t��ֵ��
�����t��ֵ��
��2������S��ϵʽ��Ҫ���������AQP�ĸߣ���ͼ����ʾ������P������P��PD��x���ڵ�D������ƽ����PD��BO������APD�ס�ABO�� ![]() ���PD���Ӷ�S�������S��t֮��ĺ�����ϵʽ��һ������t�Ķ��κ��������ö��κ�����ֵ�ķ������S�����ֵ��
���PD���Ӷ�S�������S��t֮��ĺ�����ϵʽ��һ������t�Ķ��κ��������ö��κ�����ֵ�ķ������S�����ֵ��
�������P��Q����������Sȡ���ֵʱ�����Ƴ���ʱPDΪ��OAB����λ�ߣ��Ӷ��������P���ݺ����꣬������Q�����꣬�Ӷ���õ�P��Q�����ꣻ���P��Q������֮���롰����PQ������Ķ��壨x2��x1��y2��y1�������������

 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�