题目内容
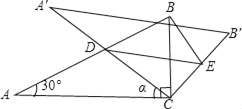
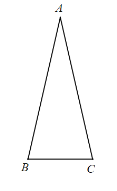
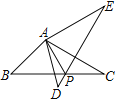
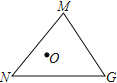
【题目】如图,△ABC 中,AB=AC, ∠BAC <60°,将线段 AB 绕点 A逆时针旋转 60°得到点 D, 点 E 与点 D 关于直线 BC 对称,连接 CD,CE,DE.
(1)依题意补全图形;
(2)判断△CDE 的形状,并证明;
(3)请问在直线CE上是否存在点 P,使得 PA - PB =CD 成立?若存在,请用文字描述出点 P 的准确位置,并画图证明;若不存在,请说明理由.

【答案】(1)见详解;(2)![]() 是等边三角形,证明见详解;(3)存在,点P在点C左边距离为CE长的位置,证明见详解.
是等边三角形,证明见详解;(3)存在,点P在点C左边距离为CE长的位置,证明见详解.
【解析】
(1)根据题意补全图形即可;
(2)连接BD、CE,由旋转的性质及对称的性质利用SAS可证![]() ,易得
,易得![]() ,可知
,可知![]() 是等边三角形;
是等边三角形;
(3)将![]() 绕点B逆时针旋转
绕点B逆时针旋转![]() 得到
得到![]() ,延长
,延长![]() 交直线CE于点P,连接BP,由旋转的性质及已知条件即可确定点P的位置.
交直线CE于点P,连接BP,由旋转的性质及已知条件即可确定点P的位置.
解:(1)如图即为所求,
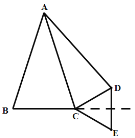
(2)![]() 是等边三角形.
是等边三角形.
如图,连接BD、CE,

由点D与点E关于直线BC对称可知BF垂直平分DE,
![]()
由旋转可知![]() ,
,
![]() 为等边三角形
为等边三角形
![]()
![]()
![]()
![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
![]()
![]() 是等边三角形;
是等边三角形;
(3)存在,
如图,将![]() 绕点B逆时针旋转
绕点B逆时针旋转![]() 得到
得到![]() ,延长
,延长![]() 交直线CE于点P,连接BP,
交直线CE于点P,连接BP,
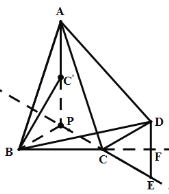
由(2)得![]() 是等边三角形,
是等边三角形,
![]()
![]()
![]()
由旋转可得![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
所以直线CE上存在点 P,使得 PA - PB =CD 成立,点P在点C左边距离为CE长的位置.

 阅读快车系列答案
阅读快车系列答案【题目】某学校初二和初三两个年级各有600名同学,为了科普卫生防疫知识,学校组织了一次在线知识竞赛,小宇分别从初二、初三两个年级随机抽取了40名同学的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
![]() .初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:
.初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
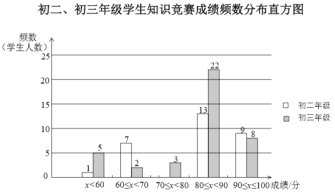
![]() .初二年级学生知识竞赛成绩在
.初二年级学生知识竞赛成绩在![]() 这一组的数据如下:
这一组的数据如下:
80 80 81 83 83 84 84 85 86 87 88 89 89
![]() .初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
.初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
初二年级 | 80.8 |
| 96.9 |
初三年级 | 80.6 | 86 | 153.3 |
根据以上信息,回答下列问题:
(1)补全上面的知识竞赛成绩频数分布直方图;
(2)写出表中![]() 的值;
的值;
(3)![]() 同学看到上述的信息后,说自己的成绩能在本年级排在前40%,
同学看到上述的信息后,说自己的成绩能在本年级排在前40%,![]() 同学看到
同学看到![]() 同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断
同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断![]() 同学是________(填“初二”或“初三”)年级的学生,你判断的理由是________.
同学是________(填“初二”或“初三”)年级的学生,你判断的理由是________.
(4)若成绩在85分及以上为优秀,请估计初二年级竞赛成绩优秀的人数为____.
【题目】某学校初二和初三两个年级各有600名同学,为了科普卫生防疫知识,学校组织了一次在线知识竞赛,小宇分别从初二、初三两个年级随机抽取了40名同学的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
![]() .初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:
.初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
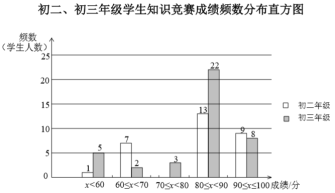
![]() .初二年级学生知识竞赛成绩在
.初二年级学生知识竞赛成绩在![]() 这一组的数据如下:
这一组的数据如下:
80 80 81 83 83 84 84 85 86 87 88 89 89
![]() .初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
.初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
初二年级 | 80.8 |
| 96.9 |
初三年级 | 80.6 | 86 | 153.3 |
根据以上信息,回答下列问题:
(1)补全上面的知识竞赛成绩频数分布直方图;
(2)写出表中![]() 的值;
的值;
(3)![]() 同学看到上述的信息后,说自己的成绩能在本年级排在前40%,
同学看到上述的信息后,说自己的成绩能在本年级排在前40%,![]() 同学看到
同学看到![]() 同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断
同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断![]() 同学是________(填“初二”或“初三”)年级的学,你判断的理由是________.
同学是________(填“初二”或“初三”)年级的学,你判断的理由是________.
(4)若成绩在85分及以上为优秀,请估计初二年级竞赛成绩优秀的人数为____.
【题目】为了迎接2022年的冬奥会,中小学都积极开展冰上运动,小乙和小丁进行500米短道速滑比赛,他们的五次成绩(单位:秒)如表所示:
1 | 2 | 3 | 4 | 5 | |
小乙 | 45 | 63 | 55 | 52 | 60 |
小丁 | 51 | 53 | 58 | 56 | 57 |
设两人的五次成绩的平均数依次为![]() 乙,
乙,![]() 丁,成绩的方差一次为
丁,成绩的方差一次为![]() ,
,![]() ,则下列判断中正确的是( )
,则下列判断中正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()