题目内容
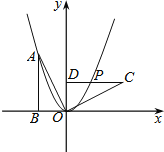
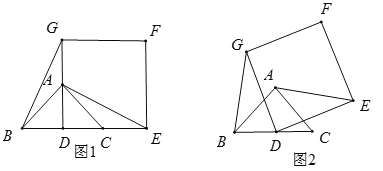
【题目】如图,将边长为![]() 的正方形放在平面直角坐标系第二象限,使
的正方形放在平面直角坐标系第二象限,使![]() 边落在
边落在![]() 轴负半轴上,且点
轴负半轴上,且点![]() 的坐标是
的坐标是![]() .
.
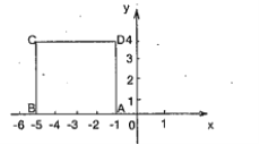
(1)直线![]() 经过点
经过点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(2)若直线![]() 经过点
经过点![]() ,且将正方形
,且将正方形![]() 分成面积相等的两部分,求直线
分成面积相等的两部分,求直线![]() 的解析式;
的解析式;
(3)若直线![]() 经过点
经过点![]() 且与直线
且与直线![]() 平行.将(2)中直线
平行.将(2)中直线![]() 沿着
沿着![]() 轴向上平移
轴向上平移![]() 个单位,交
个单位,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)10;(2)![]() ;(3)27.
;(3)27.
【解析】
(1)先求出E点的坐标,根据梯形的面积公式即可求出四边形AECD的面积;
(2)在DC上取一点G,使CG=AE=1,根据面积相等求出点G的坐标,设直线l的解析式是y=kx+b,把E、G的坐标代入即可求出解析式;
(3)根据直线l1经过点F(![]() ,0)且与直线y=-3x平行,知k=3,把F的坐标代入即可求出b的值即可得出直线11,再求出直线
,0)且与直线y=-3x平行,知k=3,把F的坐标代入即可求出b的值即可得出直线11,再求出直线![]() 沿着
沿着![]() 轴向上平移
轴向上平移![]() 个单位所得到的直线解析式,进一步求出M、N的坐标,利用三角形的面积公式即可求出△MNF的面积.
个单位所得到的直线解析式,进一步求出M、N的坐标,利用三角形的面积公式即可求出△MNF的面积.
解:(1)当![]() 时,
时,![]() ,∴
,∴![]() .
.
∴E(-2,0).
由已知,得AD=AB=BC=DC=4,AB//DC,
∴四边形AECD是梯形.
∴![]() .
.
(2)如图,在DC上取一点G,使CG=AE=1,
∴![]() ,
,
∴G点的坐标为(-4,4).
设直线L的解析式为![]() ,则
,则
![]() ,解得:
,解得:![]() .
.
∴![]() .
.
∴直线L的解析式是![]() .
.
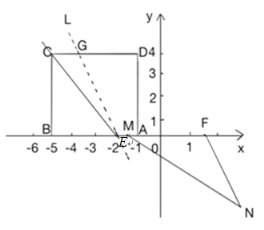
(3)∵直线![]() 经过点F(
经过点F(![]() )且与直线
)且与直线![]() 平行,设直线
平行,设直线![]() 的解析式为
的解析式为![]() ,则
,则![]() ,
,![]() ,解得
,解得![]() .
.
∴直线![]() :
:![]() .
.
将(2)中直线L沿着![]() 轴向上平移1个单位,则所得直线的解析式是
轴向上平移1个单位,则所得直线的解析式是![]() ,
,
即:![]() .
.
![]() .
.
∴![]() .
.
∴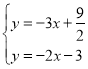 ,解得:
,解得: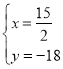 .
.
∴ ![]() .
.
∴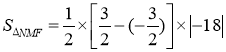 =27.
=27.
故△NMF的面积是27.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示.
销售量p(件) | P=50—x |
销售单价q(元/件) | 当1≤x≤20时,q=30+ 当21≤x≤40时,q=20+ |
(1)求该网店第x天获得的利润y关于x的函数关系式;
(2)这40天中该网店第几天获得的利润最大?最大利润是多少?