题目内容

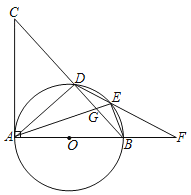
【题目】某数学课外兴趣小组为了测量池塘对岸山丘上的塔的高度,在山脚下的广场处测得建筑物点(即山顶)的抑角为,沿水平方向前进245米到达点,测得建筑物顶部点的仰角为,已知山丘高182米,求塔的高度．(结果精确到0.1米,参考数据,,)

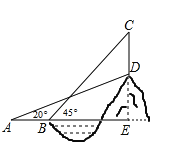
【答案】78.6米

【解析】

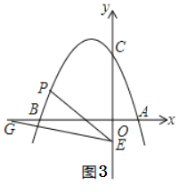
由题意可知CE⊥AE，由已知可得，设塔高高为，在直角三角形中利用，构建方程，即可求得答案.

解:由题意可知CE⊥AE,

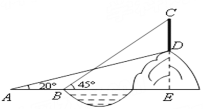
又∵∠CBE=45°

∴CE=BE

设塔CD高为x米

∴BE=CE=CD+DE=x+182

∴AE=AB+BE=245+x+182=x+427

在直角三角形AED中,即

解得:x≈78.6,

经检验:x=78.6是原方程的根,且符合题意,

答:塔CD高约为78.6米

练习册系列答案
相关题目

【题目】如图，AB是⊙O的直径，AC⊥AB，BC交⊙O于点D，点E在劣弧BD上，DE的延长线交AB的延长线于点F，连接AE交BD于点G．

（1）求证：∠AED＝∠CAD；

（2）若点E是劣弧BD的中点，求证：ED2＝EGEA；

（3）在（2）的条件下，若BO＝BF，DE＝2，求EF的长．

【题目】某单位在疫情期间用3000元购进A、B两种口罩1100个，购买A种口罩与购买B种口罩的费用相同，且A种口罩的单价是B种口罩单价的1.2倍；

（1）求A，B两种口罩的单价各是多少元?

（2）若计划用不超过7000元的资金再次购进A、B两种口罩共2600个，已知A、B两种口罩的进价不变，求A种口罩最多能购进多少个?

【题目】学校与图书馆在同一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达目的地，两人之间的距离y （米）与时间t （分钟）之间的函数关系如图所示，根据图象信息知，点A的坐标是__________；

【题目】已知抛物线y＝ax2＋bx＋3经过点A （1，0）和点B （－3，0），与y轴交于点C，点P为第二象限内抛物线上的动点．

（1）抛物线的解析式为__________，抛物线的项点坐标为__________；

（2）如图1，是否存在点P，使四边形BOCP的面积为8?若存在，请求出点P的坐标；若不存在，请说明理由．

（3）如图2，连接OP交BC于点D，当S△CPD∶S△BPD＝1∶2时，请求出点D的坐标；

（4）如图3，点E的坐标为（0，－1），点G为x轴负半轴上的一点，∠OGE＝15°，连接PE，若∠PEG＝2∠OGE，请求出点P的坐标．

【题目】八个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线将这八个正方形分成面积相等的两部分，则该直线的解析式为（ ）

A. B. C. D.

【题目】如图，在平面直角坐标系xOy中，直线y=﹣x+4与坐标轴交于A，B两点，OC⊥AB于点C，P是线段OC上的一个动点，连接AP，将线段AP绕点A逆时针旋转45°，得到线段AP'，连接CP'，则线段CP'的最小值为(　　)

A.B.1C.D.

【题目】如图，在△ABC中，AB=BC，以BC为直径作⊙ O交AC于点E，过点E作AB的垂线交AB于点F，交CB的延长线于点G．

（1）求证：EG是⊙O的切线；

（2）若BG=OB，AC=6，求BF的长．

【题目】某学校七年级共有500名学生，为了解该年级学生的课外阅读情况，将从中随机抽取的40名学生一个学期的阅读量(阅读书籍的本数)作为样本，根据数据绘制了如下的表格和统计图：

等级

阅读量(本)

频数

频率

E

x≤2

4

0.1

D

2<x≤4

12

0.3

C

4<x≤6

a

0.35

B

6<x≤8

c

b

A

x>8

4

0.1

根据上面提供的信息，回答下列问题：

(1)统计表中的 ， ；并补全条形统计图；

(2)根据抽样调查结果，请估计该校七年级学生一学期的阅读量为“等”的有多少人?

(3)样本中阅读量为“等”的4名学生中有2名男生和2名女生，现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动，请用树状图法或列表法求出恰好选中“1男1女”的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网