题目内容

如图，直线与双曲线相交于M、N点，其横坐标分别为1和3，则不等式的解集是       。
-3＜x＜-1

试题分析：如图，直线与双曲线相交于M、N点，其横坐标分别为1和3，不等式变形为，其解集从图形上来看就是直线的图象要高于双曲线的图象，观察图象得-3＜x＜-1
点评：本题考查直线和双曲线，掌握直线和双曲线的性质是解答本题的关键，要求学生能通过观察图象来求解不等式的解集
练习册系列答案
相关题目
如图，M为双曲线上的一点，过点Ｍ作ｘ轴、ｙ轴的垂线，分别交直线ｙ＝－2ｘ＋m于D、C两点，若直线ｙ＝－2ｘ＋m与ｙ轴交于点Ａ，与ｘ轴相交于点B．则AD·BC的值为　 　
如图，在平面直角坐标系中,一次函数的图象与轴交于点Ａ,与轴交于点Ｂ,与反比例函数的图象分别交于点Ｍ、Ｎ，已知△AOB的面积为1，点Ｍ的纵坐标为2.

（1）求一次函数与反比例函数的解析式；
（2）直接写出＞时,的取值范围.
如图，一次函数的图象与反比例函数（x＜0）的图象相交于A点，与y轴、x轴分别相交于B、C两点，且C（2，0），A点的横坐标为-1.

（1）求一次函数的解析式；
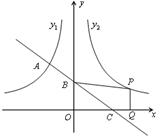
（2）设函数（x＞0）的图象与（x＜0）的图象关于y轴对称，在（x＞0）的图象上取一点P（P点的横坐标大于2），过P点作PQ⊥x轴，垂足是Q，若四边形BCQP的面积等于2，求P点的坐标．
已知一次函数y=kx+b的图象经过点A（－1，3）和点B(2，－3)．
（1）求这个一次函数的解析式；
（2）当x取何值时，函数值？
甲、乙两车从A地将一批物品匀速运往B地，甲出发0.5h后乙开始出发，结果比甲早1h到达B地．甲车离A地的路程s1（km）与行驶的时间t（h）之间的函数关系，如图中线段OP所示；乙车离A地的路程s2（km）与行驶的时间t（h）之间的函数关系，如图中线段MN所示，a表示A、B两地之间的距离．请结合图中的信息解决如下问题：

（1）分别求出线段MN、OP的函数关系式；
（2）求出a的值；
（3）设甲、乙两车之间的距离为s（km），求s与甲车行驶时间t（h）的函数关系式，并求出s的最大值．
水产养殖专业户王大爷承包了30亩水塘，分别养殖甲鱼和桂鱼．有关成本、销售额见右表：

（1）2012年，王大爷养殖甲鱼20亩，桂鱼10亩．求王大爷这一年共收益多少万元？（收益＝销售额－成本）
（2）2013年，王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼，计划投入成本不超过70万元．若每亩养殖的成本、销售额与2012年相同，要获得最大收益，他应养殖甲鱼和桂鱼各多少亩？
（3）已知甲鱼每亩需要饲料500kg，桂鱼每亩需要饲料700kg．根据(2)中的养殖亩数，为了节约运输成本，实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍，结果运输养殖所需全部饲料比原计划减少了2次．求王大爷原定的运输车辆每次可装载饲料多少kg?
如右图，一次函数y＝kx＋b的图象经过A、B两点，则不等式kx＋b < 0的解集是          
若一次函数y=2x+l的图象与反比例函数图象的一个交点横坐标为l，则反比例函数关系式为               .

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网