题目内容
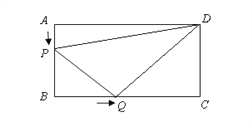
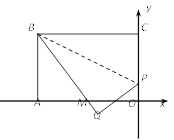
【题目】如图,已知矩形OABC的顶点A在x轴的负半轴上,顶点C在y轴上,且AB=4.P为OC上一点,将△BCP沿PB折叠,点C落在第三象限内点Q处,BQ与x轴的交点M恰好为OA的中点,且MQ=1.
(1)求点A的坐标;
(2)求折痕PB所对应的函数表达式.
【答案】(1) A(-6,0);(2) y=-![]() x+1.
x+1.
【解析】
(1)由M为OA的中点,可设AM=OM=x.根据矩形的性质得出BC=AO=2x.由折叠的性质得出BQ=BC=2x,那么BM=2x-1.在Rt△ABM中根据勾股定理列出方程x2+42=(2x-1)2,解方程求出x,进而得到点A的坐标;
(2)设PQ与OA相交于点N.由△MQN∽△MAB,求出MN=![]() ,QN=
,QN=![]() ,那么ON=
,那么ON=![]() .由△MQN∽△PON,求出OP=1,得到P(0,1).设折痕PB所对应的函数表达式为y=kx+b,将B、P两点的坐标代入,利用待定系数法即可求出折痕PB所对应的函数表达式.
.由△MQN∽△PON,求出OP=1,得到P(0,1).设折痕PB所对应的函数表达式为y=kx+b,将B、P两点的坐标代入,利用待定系数法即可求出折痕PB所对应的函数表达式.
解:(1)∵M为OA的中点,
∴可设AM=OM=x.
∵四边形OABC是矩形,
∴BC=AO=2x.
由△BCP沿PB折叠,得BQ=BC=2x,则BM=BQ-MQ=2x-1.
在Rt△ABM中,由勾股定理得x2+42=(2x-1)2,
解得x=3,
∴A(-6,0);
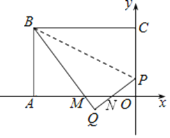
(2)如图,设PQ与OA相交于点N.
在△MQN与△MAB中,![]() ,
,
∴△MQN∽△MAB,
∴![]() ,即
,即![]() ,
,
∴MN=![]()
,QN=![]() .
.
∴ON=OM-MN=3-![]() =
=![]() .
.
在△MQN与△PON中,
![]() ,
,
∴△MQN∽△PON,
∴![]() ,即
,即![]() ,
,
∴OP=1,∴P(0,1).
设折痕PB所对应的函数表达式为y=kx+b,
∵B(-6,4)、P(0,1),
∴-6k+b=4,b=1,解得k=-![]() ,b=1,
,b=1,
∴折痕PB所对应的函数表达式为y= -![]() x+1.
x+1.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目