题目内容
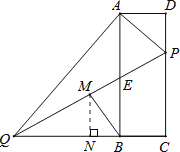
【题目】如图，在矩形ABCD中，点P在边CD上，且与C、D不重合，过点A作AP的垂线与CB的延长线相交于点Q，连接PQ，M为PQ中点．
（1）求证：△ADP∽△ABQ；
（2）若AD=10，AB=20，点P在边CD上运动，设DP=x，BM2=y，求y与x的函数关系式，并求线段BM的最小值；
【答案】(1)证明见解析；（2）y=
x2-20x+125（0＜x＜20）．
．
【解析】
试题分析：（1）由对应两角相等，证明两个三角形相似；
（2）如解答图所示，过点M作MN⊥QC于点N，由此构造直角三角形BMN，利用勾股定理求出y与x的函数关系式，这是一个二次函数，求出其最小值；
试题解析：（1）∵∠QAP=∠BAD=90°，
∴∠QAB=∠PAD，
又∵∠ABQ=∠ADP=90°，
∴△ADP∽△ABQ．
（2）∵△ADP∽△ABQ，
∴
，即
，解得QB=2x．
∵DP=x，CD=AB=20，
∴PC=CD-DP=20-x．
如图所示，过点M作MN⊥QC于点N，
∵MN⊥QC，CD⊥QC，点M为PQ中点，
∴点N为QC中点，MN为中位线，
∴MN=
PC=（20-x）=10-x，
BN=QC-BC=（BC+QB）-BC=（10+2x）-10=x-5．
在Rt△BMN中，由勾股定理得：BM2=MN2+BN2=（10-x）2+（x-5）2=x2-20x+125，
∴y=x2-20x+125（0＜x＜20）．
∵y=x2-20x+125=（x-8）2+45，
∴当x=8即DP=8时，y取得最小值为45，BM的最小值为
=．
练习册系列答案
相关题目
