Question

【题目】如图1，两个形状、大小完全相同的含有30°，60°的三角板按如图所示放置，PA、PB与直线MN重合，且三角板PAC和三角板PBD均可以绕点P逆时针旋转。

（1）如图2，若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度，PF平分∠APD，PE平分∠CPD，求∠EPF的度数。

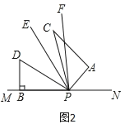
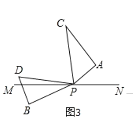
（2）如图3，若三角板PAC的边PA从PN处开始绕点P逆时针旋转，转速为3°/s，同时三角板PBD的边PB从PM处开始绕点P逆时针旋转，转速为2°/s。在两块三角板旋转过程中(PC转到PM重合时，两三角板都停止转动)，设两块三角板旋转的时间为ts,则∠BPN= °，∠CPD= °（用含t的式子表示，并化简）；以下两个结论：①为定值；②∠BPN+∠CPD为定值，正确的是 （填序号）。

Answer 1

【答案】（1）∠EPF=30゜；（2）（180－2t），（90－t）；①．

【解析】

（1）设∠CPE=∠DPE=x，∠CPF=y，则∠APF=∠DPF=2x+y，进而利用∠CPA=60゜求出即可；

（2）设运动时间为t秒，则∠BPM=2t，即可表示出∠CPD和∠BPN的度数，然后再代入①②中计算即可得出答案．

解：（1）如图2，设∠CPE=∠DPE=x，∠CPF=y，

则∠APF=∠DPF=2x+y，

∵∠CPA=60゜，

∴y+2x+y=60゜，

∴x+y=30゜，

∴∠EPF=x+y=30゜.

（2）由题意得∠BPM=2t，

∴∠BPN=180－2t，∠DPM=30－2t，∠APN=3t．

∴∠CPD=180－∠DPM－∠CPA－∠APN=90－t，

∴，所以①正确．

因为∠BPN+∠CPD=180－2t+90－t=270－3t，可以看出∠BPN+∠CPD随着时间t的变化而变化，不为定值，所以结论②错误．

故答案为：（180－2t），（90－t）；①．