题目内容
【题目】在平面直角坐标系 xoy 中,已知点 A 的坐标为(-2,0).
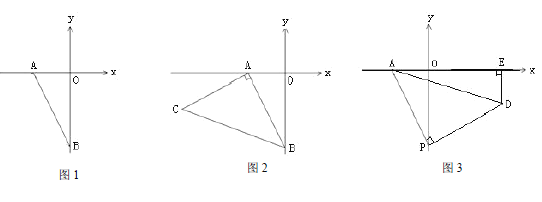
(1)如图 1,当点 B 的坐标为(0,-4)时,则△AOB 的面积是 ;
(2)如图 2,在(1)的条件下,过点 A 作 AC⊥AB,且使 AC=AB,求第三象限内的点 C 的坐标;
(3)如图 3,P 为 y 轴负半轴上一点,过点 P 作 PD⊥PA,且使 PD=PA,过第四象限内的点 D 作 DE⊥x 轴于 E,试判断 OP-DE 的值是否发生变化.若不发生变化,请求其值;若发生变化,请说明理由.
【答案】(1)4;(2)点C坐标为(-6,-2);(3)![]() 的值不发生变化,其值为2, 证明见解析
的值不发生变化,其值为2, 证明见解析
【解析】
(1)由A(-2,0),B(0,-4)可得OA、OB的长度,利用三角形的面积公式进行计算即可得出答案;
(2)作CD⊥AD,易证∠ACD=∠OAB,即可求证△ACD≌△BAO,可得AD=OB,CD=OA即可解题;
(3)作DF⊥OP,易证∠APO=∠PDF,即可证明△AOP≌△PFD,可得AO=PF,DE=OF,即可解题.
(1)∵A(-2,0),B(0,-4)
∴OA=2,OB=4
∴△AOB 的面积是:![]()
故答案为:4
(2)如图,
过点C作CD⊥AD,
∴∠ADC=∠AOB=90°,
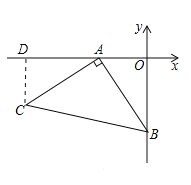
∵∠CAD+∠ACD=90°,∠CAD+∠OAB=90°,
∴∠ACD=∠OAB,
在△ACD和△BAO中,
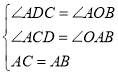
∴△ACD≌△BAO,(AAS)
∴AD=OB,CD=OA,
∴OD=6,CD=2
∴点C坐标为(-6,-2);
(3) OP-DE的值不发生变化,其值为2,理由如下:
作DF⊥OP,
∴∠AOP=∠PFD=90°,
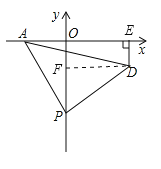
∵∠APO+∠DPF=90°,∠PDF+∠DPF=90°,
∴∠APO=∠PDF,
在△AOP和△PFD中,
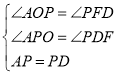
∴△AOP≌△PFD,(AAS)
∴AO=PF,
∵DE⊥x轴
∴∠OED=90°
∴∠OED=∠FOE=∠OFD=90°
∴四边形OFDE是矩形
∴DE=OF,
∴OP-DE=OP-OF=FP=AO=2

【题目】下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:
考试类别 | 平时考试 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩(分) | 85 | 78 | 90 | 91 | 90 | 94 |
(1)小明6次成绩的众数是 ,中位数是 ;
(2)求该同学这个同学这一学期平时成绩的平均数;
(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分?
【题目】我市一水果销售公司,需将一批鲜桃运往某地,有汽车、火车、运输工具可供选择,两种运输工具的主要参考数据如下:
运输工具 | 途中平均速度(单位:千米/时) | 途中平均费用(单位:元/千米) | 装卸时间(单位:小时) | 装卸费用(单位:元) |
汽车 | 75 | 8 | 2 | 1000 |
火车 | 100 | 6 | 4 | 2000 |
若这批水果在运输过程中(含装卸时间)的损耗为150元/时,设运输路程为x(![]() )千米,用汽车运输所需总费用为y1元,用火车运输所需总费用为y2元.
)千米,用汽车运输所需总费用为y1元,用火车运输所需总费用为y2元.
(1)分别求出y1、y2与x的关系式;
(2)那么你认为采用哪种运输工具比较好?




