题目内容
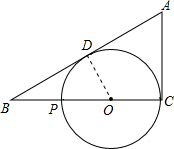
如图,已知AC切⊙O于C点,CP为⊙O的直径,AB切⊙O于D与CP的延长线交于B点,若AC=PC.
求证:(1)BD=2BP;(2)PC=3BP.

求证:(1)BD=2BP;(2)PC=3BP.

证明:(1)连接OD,
∵D、C是切点,PC是直径,OD是半径,
∴∠BDO=∠ACB=90°,
又∠B=∠B,
∴△BDO∽△BCA,(1分)
∴
=
,
∵AC=PC=2OD,
∴BD=
BC.①(2分)
又BD2=BP•BC,②(3分)
②÷①,得BD=2BP.(4分)
(2)由BD2=BP•BC,
又∵BC=BP+PC,BD=2BP,
∴4BP2=BP(BP+PC),(5分)
∴4BP=BP+PC,
∴PC=3BP.(6分)
∵D、C是切点,PC是直径,OD是半径,
∴∠BDO=∠ACB=90°,
又∠B=∠B,
∴△BDO∽△BCA,(1分)
∴
| BD |
| BC |
| OD |
| AC |
∵AC=PC=2OD,
∴BD=
| 1 |
| 2 |
又BD2=BP•BC,②(3分)
②÷①,得BD=2BP.(4分)
(2)由BD2=BP•BC,
又∵BC=BP+PC,BD=2BP,
∴4BP2=BP(BP+PC),(5分)
∴4BP=BP+PC,
∴PC=3BP.(6分)


练习册系列答案
相关题目







