��Ŀ����
����Ŀ����ͼ���ڡ�ABC�У���BAC=90�㣬AB=AC����DΪֱ��BC��һ�����㣬����D��ҪB��C�غϣ�����ADΪ����AD���ϱ���������ADEF������CF��
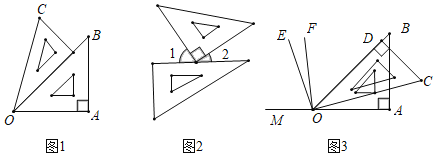
��1���۲���룺��ͼ1������D���߶�BC��ʱ����BC��CF��λ�ù�ϵΪ_____����AC��CD��CF֮���������ϵΪ_____��
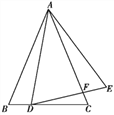
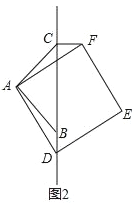
��2����ͼ2������D���߶�CB���ӳ�����ʱ�����Ϣ����ڹ�ϵ�Ƿ������������ȥ�������֤����������������д����ȷ�Ľ��ۣ���˵�����ɣ�
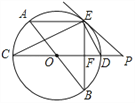
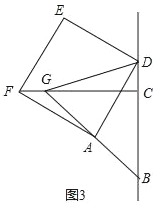
��3����ͼ3������D���߶�BC���ӳ�����ʱ���ӳ�BA��CF�ڵ�G������GD����AB=2![]() ��CD=
��CD=![]() BC�����DG�ij���
BC�����DG�ij���
���𰸡� BC��CF CF+CD=![]() AC
AC
����������������1����֤����BAD=��CAF����SAS֤����BAD�ա�CAF���ó���ACF=��ABD=45�㣬֤����ACF+��ACB=90�㣬���ɵó����ۣ�����ȫ�������ε����ʵó�BD=CF��֤��CF=BC-CD���ɣ�(2)����֤����BAD=��CAF����SAS֤����BAD�ա�CAF���ó���ACF=��ABD=180��-45��=135�㣬֤����ACB+��FCB=135�㣬�ó���FCB=90�㣬���ɵó����ۣ�
����ȫ�������ε����ʵó�BD=CF��֤��CF=CD-BC���ɣ�(3)����SAS֤����BAD�ա�CAF���ó���ACF=��ABD=45�㣬֤����FCB=��ACF+��ACB=90�㣬�ó�CF��BC����Rt��ABC�У��ɹ��ɶ����ó�AC=AB=2![]() ����Rt��AGC�У��ó�CG=
����Rt��AGC�У��ó�CG=![]() AC=4��ͬ��BC=4��CD=
AC=4��ͬ��BC=4��CD=![]() BC=1����Rt��DCG�У��ɹ��ɶ����������DG�ij���
BC=1����Rt��DCG�У��ɹ��ɶ����������DG�ij���
��⣺��1���١ߡ�BAC=90�㣬AB=AC�����ABC=��ACB=45�㣬���ı���ADEF�������Σ�
��AD=AF����DAF=90�㣬�ߡ�BAC=��BAD+��DAC=90�㣬��DAF=��CAF+��DAC=90�㣬
���BAD=��CAF���ڡ�BAD�͡�CAF�У�AB=AC����BAD=��CAF��AD=AF��
���BAD�ա�CAF��SAS�������ACF=��ABD=45�㣬���ACF+��ACB=90�㣬���BCF=90�㣬
��BC��CF��
�ڡߡ�BAD�ա�CAF����BD=CF����BD+CD=BC����CF+CD=BC���֡�Rt��ABC�У�BC=![]() AC��
AC��
��CF+CD=![]() AC��
AC��
��2���ٳ������ڲ���������ȷ�Ľ���ΪCD��CF=![]() AC��
AC��
���ɣ��١ߡ�BAC=90�㣬AB=AC�����ABC=��ACB=45�㣬���ı���ADEF�������Σ�
��AD=AF����DAF=90�㣬�ߡ�BAC=��BAF+��FAC=90�㣬��DAF=��BAF+��DAB=90�㣬
���BAD=��CAF���ڡ�BAD�͡�CAF�У�AB=AC����BAD=��CAF��AD=AF��
AB=AC����BAD=��CAF��AD=AF�� ���BAD�ա�CAF��SAS����
���ACF=��ABD=180�㩁45��=135�㣬���ACB+��FCB=135�㣬 ���FCB=90�㣬 ��BC��CF��
�ڡߡ�BAD�ա�CAF����BD=CF����CD��BD=BC��CD��CF=BC��
�֡�Rt��ABC�У�BC=![]() AC�� ��CD��CF=
AC�� ��CD��CF=![]() AC��
AC��
��3��������ã���BAC=��FAD=90�㣬 ���BAD=��CAF��
�ڡ�BAD�͡�CAF�У�AB=AC����BAD=��CAF��AD=AF�����BAD�ա�CAF��SAS����
���ACF=��ABD=45�㣬���FCB=��ACF+��ACB=45��+45��=90�㣬��CF��BC��
��Rt��ABC�У�AC=AB=2![]() ��BC=4����Rt��AGC�У��ߡ�ACF=45�㣬
��BC=4����Rt��AGC�У��ߡ�ACF=45�㣬
��CG=![]() AC=
AC=![]() ��2
��2![]() =4�� ��CD=
=4�� ��CD=![]() BC=
BC=![]() ��4=1��
��4=1��
����Rt��DCG��DG=![]() ��
��