题目内容
【题目】如图,在△ABC中,AB=AC,CE平分∠ACB交AB于点E,CE=BC.
(1)求∠A的度数;
(2)能否在AC边上找一点D,并连接ED,使△AED≌△CEB?若能,请作出你找的点,并证明;若不能,请说明理由.

【答案】(1)36°;(2)见解析.
【解析】
(1)根据等腰三角形的性质,三角形内角和定理和角平分线的性质即可解答本题;
(2)根据(1)中的结论和全等三角形的判定即可解答.
解:(1)∵在△ABC中,AB=AC,
∴∠B=∠ACB,
∵CE平分∠ACB交AB于点E,CE=BC,
∴∠ECA=∠ECB,∠B=∠CEB,
∴∠CEB=∠ACB,
∵∠CEB=∠A+∠ECA,
∴∠A=∠ECA,
设∠A=x,则∠B=∠ACB=2x,
x+2x+2x=180°,
解得,x=36°,
∴∠A=36°;
(2)在AC边上存在一点D,并连接ED,使△AED≌△CEB,作ED∥BC交AC于点D,点D即为所求,
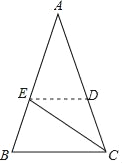
证明:由(1)知∠A=∠ECA,
∴AE=EC,
∵ED∥BC,
∴∠AED=∠B,
∴∠AED=∠CEB,
在△AED和△CEB中,
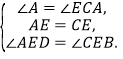
∴△AED≌△CEB(ASA).
故答案为:(1)36°;(2)见解析.

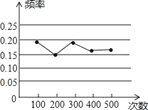
【题目】为了了解某一景点等候检票的时间,随机调查了部分游客,统计了他们进入该景点等候检票的时间,并绘制成如图表.
等候时间x(min) | 频数(人数) | 频率 |
10≤x<20 | 8 | 0.2 |
20≤x<30 | 14 | a |
30≤x<40 | 10 | 0.25 |
40≤x<50 | b | 0.125 |
50≤x<60 | 3 | 0.075 |
合计 | 40 | 1 |
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)表中a= ,b= ,并请补全频数分布直方图;
(3)根据上述图表制作扇形统计图,则“40≤x<50”所在扇形的圆心角度数是 °.