题目内容
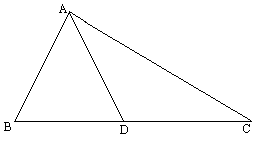
如图所示,AD是∠BAC的角平分线,若∠ADC=![]() ,且∠DAC=∠C,求△ABC的三个内角的度数.
,且∠DAC=∠C,求△ABC的三个内角的度数.
答案:
解析:
解析:
|
解:∵∠ADC= 且∠ADC+∠DAC+∠C= ∴∠C=∠DAC= ∵AD是△ABC的平分线, ∴∠BAD=∠DAC= ∴∠BAC= 又∠BAC+∠B+∠C= ∴∠B= ∴在△ABC中,∠BAC= 分析:因为∠ADC= 点拨:由于此题要求的三角形三个内角全都是未知,那么我们就要从已知出发,找出突破口.先求出一个内角度数.从而进一步运用定理解答,使未知逐个清晰、明了. |

练习册系列答案
相关题目
 如图所示,AD是△ABC中BC边上的中线,已知△ABC的面积为12,则△ACD的面积等于
如图所示,AD是△ABC中BC边上的中线,已知△ABC的面积为12,则△ACD的面积等于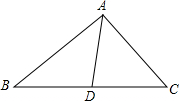 如图所示,AD是△ABC的中线,AB=6cm,AC=5cm,求△ABD和△ADC的周长的差.
如图所示,AD是△ABC的中线,AB=6cm,AC=5cm,求△ABD和△ADC的周长的差. 55、如图所示,AD是∠BAC的平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且BD=CD.
55、如图所示,AD是∠BAC的平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且BD=CD. 26、已知如图所示,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F,四边形AEDF是菱形吗?说明理由.
26、已知如图所示,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F,四边形AEDF是菱形吗?说明理由. 如图所示,AD是△ABC的高,AE是⊙O的直径,A,B,C三点都在圆上,∠DAC=30°,则∠BAE为( )
如图所示,AD是△ABC的高,AE是⊙O的直径,A,B,C三点都在圆上,∠DAC=30°,则∠BAE为( )