题目内容
如图所示，AD是△ABC的高，AE是⊙O的直径，A，B，C三点都在圆上，∠DAC=30°，则∠BAE为（ ）分析：首先连接BE，由AE是⊙O的直径，AD是△ABC的高，易求得∠BAE=∠DAC．
解答：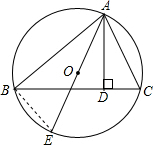
解：连接BE，
∵AE是⊙O的直径，
∴∠ABE=90°，
∴∠BAE=90°-∠E，
∵AD是△ABC的高，
∴∠ADC=90°，
∴∠DAC=90°-∠C，
∵∠E=∠C，
∴∠BAE=∠DAC=30°．
故选B．
解：连接BE，∵AE是⊙O的直径，
∴∠ABE=90°，
∴∠BAE=90°-∠E，
∵AD是△ABC的高，
∴∠ADC=90°，
∴∠DAC=90°-∠C，
∵∠E=∠C，
∴∠BAE=∠DAC=30°．
故选B．
点评：此题考查了圆周角定理与直角三角形的性质．此题比较简单，注意掌握辅助线的作法，注意数形结合思想的应用．
练习册系列答案
相关题目
如图所示，AD是△ABC中BC边上的中线，已知△ABC的面积为12，则△ACD的面积等于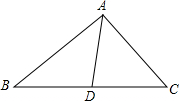
如图所示，AD是△ABC的中线，AB=6cm，AC=5cm，求△ABD和△ADC的周长的差．
55、如图所示，AD是∠BAC的平分线，DE⊥AB，垂足为E，DF⊥AC，垂足为F，且BD=CD．
26、已知如图所示，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F，四边形AEDF是菱形吗？说明理由．