题目内容
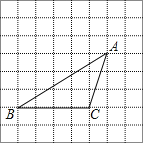
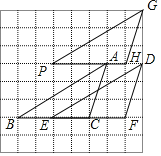
【题目】如图,将方格纸中的三角形ABC先向右平移2格得到三角形DEF,再将三角形DEF向上平移3格得到三角形GPH.
(1)动手操作:按上面步骤作出经过两次平移后分别得到的三角形;
(2)设AC与DE相交于点M,则图中与∠BAC相等的角有 个;
(3)若∠BAC=43°,∠B=32°,则∠PHG= °.
【答案】(1)见解析(2)4(3)105
【解析】
(1)利用网格特点和平移的性质画图;
(2)利用平移的性质得到∠BAC=∠EDF=∠PGH,由AB∥DE,然后利用平行线的性质得到∠BAC=∠AMD=∠CME;
(3)根据平移的性质得到∠PGH=∠BAC=43°,∠GPH=∠B=32°,然后根据三角形内角和计算∠PHG的度数.
解:(1)如图,△DEF和△GPH为所作;
(2)∠BAC=∠EDF=∠PGH,∠BAC=∠AMD=∠CME,
即图中与∠BAC相等的角有4个;
(3) ∵△ABC经过平移得到△GPH,
∴△ABC≌△GPH,
∴∠PGH=∠BAC=43°,∠GPH=∠B=32°,
∴∠PHG=180°43°32°=105°.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目