题目内容
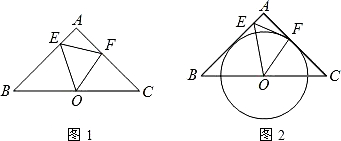
如图1所示,在△ABC中,AE是∠BAC的平分线,∠B<∠C,F为AD上一点,且FD⊥BC于D.
(1)试推导∠EFD与∠B、∠C的大小关系.
(2)如图2所示,当点F在AE的延长线上时,其余条件不变,在(1)中推导的结论还成立吗?请说明理由.

(1)试推导∠EFD与∠B、∠C的大小关系.
(2)如图2所示,当点F在AE的延长线上时,其余条件不变,在(1)中推导的结论还成立吗?请说明理由.

分析:(1)根据三角形的内角和定理和角平分线的定义表示出∠BAE,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠AEC,然后根据直角三角形两锐角互余列式计算即可得解;
(2)与(1)的求解过程完全相同.
(2)与(1)的求解过程完全相同.
解答:解:(1)∠EFD=
(∠C-∠B).
理由如下:∵AE是∠BAC的平分线,
∴∠BAE=
∠BAC=
(180°-∠B-∠C),
在△ABE中,∠AEC=∠BAE+∠B=
(180°-∠B-∠C)+∠B=90°+
∠B-
∠C,
∵FD⊥BC,
∴∠EFD=90°-(90°+
∠B-
∠C)=
(∠C-∠B);
(2)仍然成立.
又(1)知∠DEF=∠AEC=90°+
∠B-
∠C,
∴∠EFD=
(∠C-∠B).
| 1 |
| 2 |
理由如下:∵AE是∠BAC的平分线,
∴∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
在△ABE中,∠AEC=∠BAE+∠B=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵FD⊥BC,
∴∠EFD=90°-(90°+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)仍然成立.
又(1)知∠DEF=∠AEC=90°+
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EFD=
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,角平分线的定义,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目