题目内容
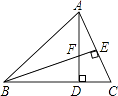
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
【答案】
(1)证明:∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,
∴△ACD∽△BFD.
(2)解:∵tan∠ABD=1,∠ADB=90°
∴ ![]() =1,
=1,
∴AD=BD,
∵△ACD∽△BFD,
∴ ![]() =
= ![]() =1,
=1,
∴BF=AC=3.
【解析】本题考查相似三角形的判定和性质、三角函数等知识,解题的关键是熟练掌握相似三角形的判定和性质,属于中考常考题型.(1)由∠C+∠DBF=90°,∠C+∠DAC=90°,推出∠DBF=∠DAC,由此即可证明.(2)先证明AD=BD,由△ACD∽△BFD,得 ![]() =
= ![]() =1,即可解决问题.
=1,即可解决问题.

练习册系列答案
相关题目